Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung:

Aufgabe 354: Volumen, Normalen und Schwerpunkt eines Körpers im Vektorfeld

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Im $ \mathbb{R}^3$ sei der Körper $ M$, der durch den Graph $ S$ der Funktion $ f(x,y) =-x^2-2x-y^2+5$ und der Ebene $ E$ mit der Gleichung $ z=1$ eingeschlossen wird, gegeben.

Das Vektorfeld $ g: \mathbb{R}^3\mapsto\mathbb{R}^3$ sei definiert durch

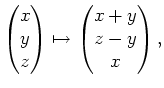
$\displaystyle \begin{pmatrix}x\\ y\\ z\end{pmatrix}\mapsto \begin{pmatrix}x+y \\ z-y \\ x \end{pmatrix},$

und die Kurve $ K$ sei gegeben durch $ S \cap E$.

a)
Wie lautet der nach außen weisende Normaleneinheitsvektor von $ \partial M$ in $ (0,0,5)$?

\fbox{\parbox{5cm}{\rule[-1.5ex]{0pt}{0.8cm}\hfill \hspace{\fill}}}        

b)
Wie lautet der nach außen weisende Normaleneinheitsvektor von $ \partial M$ in $ (-2,1,1)$?

\fbox{\parbox{5cm}{\rule[-1.5ex]{0pt}{0.8cm}\hfill \hspace{\fill}}}        

c)
$ \mathrm{rot} g = \fbox{\parbox{5cm}{\rule[-1.5ex]{0pt}{0.8cm}\hfill \hspace{\fill}}}$.

d)
$ \mathrm{div} g = \fbox{\parbox{5cm}{\rule[-1.5ex]{0pt}{0.8cm}\hfill \hspace{\fill}}}$.

e)
Eine Parametrisierung von $ K$ lautet $ v=\fbox{\parbox{5cm}{\rule[-1.5ex]{0pt}{0.8cm}\hfill \hspace{\fill}}}$.

f)
Verwenden Sie der Geometrie des Körpers angepasste Zylinderkoordinaten und ergänzen Sie das Dreifach-Integral so, dass es das Volumen von $ M$ beschreibt:

$\displaystyle \int\limits_{\ \fbox{\parbox{1.5cm}{\rule[-1.5ex]{0pt}{0.5cm}\hfi... ...ox{2cm}{\rule[-1.5ex]{0pt}{0.8cm}\hfill \hspace{\fill}}}\quad d\varphi\,dr\,dz$

g)
Das Volumen von $ M$ ist \fbox{\parbox{2cm}{\rule[-1.5ex]{0pt}{0.8cm}\hfill \hspace{\fill}}}.

h)
Sei $ S_P$ der geometrische Schwerpunkt von $ M$.

     $ x_{S_P} = \fbox{\parbox{2cm}{\rule[-1.5ex]{0pt}{1cm}\hfill \hspace{\fill}}}\;,\quad y_{S_P}= \fbox{\parbox{2cm}{\rule[-1.5ex]{0pt}{1cm}\hfill \hspace{\fill}}}$,      $ z_{S_P}=\fbox{\parbox{2cm}{\rule[-1.5ex]{0pt}{1cm}\hfill \hspace{\fill}}}$

i)
$ \iint\limits_{\partial M} g \cdot n\, \mathrm{d}O = \fbox{\parbox{2cm}{\rule[-1.5ex]{0pt}{0.8cm}\hfill \hspace{\fill}}}$.

(Hierbei sei $ n$ der nach außen weisende Normaleneinheitsvektor.)

j)
$ \int_K g \mathrm{d}x =\fbox{\parbox{2cm}{\rule[-1.5ex]{0pt}{0.8cm}\hfill \hspace{\fill}}}$.

(Aus: HM III mach, bau, umw WS 2002/03)

Lösung:

[Verweise]
  automatisch erstellt am 2.  9. 2005