Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Unterräume

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Entscheide jeweils, ob $ U$ ein Unterraum von $ V$ über dem Körper $ K$ ist. Bestimme gegebenenfalls eine Basis und die Dimension von $ U$.
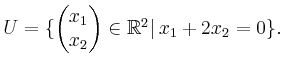
  1. $ K = \mathbb{R}$, $ V=\mathbb{R}^2$, $ U=\{\begin{pmatrix}x_1 \\ x_2\end{pmatrix}\in\mathbb{R}^2\vert\, x_1+2x_2=0\}.$
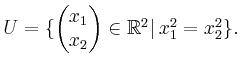
  2. $ K = \mathbb{R}$, $ V=\mathbb{R}^2$, $ U=\{\begin{pmatrix}x_1 \\ x_2\end{pmatrix}\in\mathbb{R}^2\vert\, x_1^2=x_2^2\}.$
  3. $ V=K[X]$, $ U=K[X]_{\leq n}:=\{\sum_{k=0}^n a_k X^k\vert\, a_0,\dots,a_n\in K\}$, wobei $ n\in\mathbb{N}$ fest sei.
  4. $ V=K[X]_{\leq n}$, $ U=\{p\in V\,\vert\, p(0)=0\; \mathrm{ und }\; p(1) = 0\}$.

Lösung.

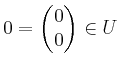  1. Wir prüfen zuerst nach, ob $ U$ ein Unterraum von $ V$ ist. Zunächst ist $ 0=\begin{pmatrix}0 \\ 0\end{pmatrix}\in U$, weil $ 0+2\cdot 0=0$.

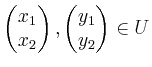    Seien nun $ \begin{pmatrix}x_1 \\ x_2\end{pmatrix},\begin{pmatrix}y_1 \\ y_2\end{pmatrix}\in U$ und $ \lambda,\mu\in K$. Folglich gelten $ x_1+2x_2=0$ und $ y_1+2y_2=0$. Es wird

    $\displaystyle (\lambda x_1+\mu y_1)+2(\lambda x_2+\mu y_2) \;=\; \lambda (x_1+2x_2)+\mu(y_1+2y_2) \;=\; 0\;, $

    und daher gilt

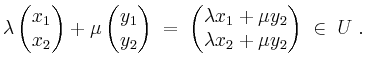
    $\displaystyle \lambda\begin{pmatrix}x_1 \\ x_2\end{pmatrix} + \mu\begin{pmatrix... ...n{pmatrix}\lambda x_1+\mu y_2 \\ \lambda x_2+\mu y_2\end{pmatrix} \;\in\; U\;. $

    Also ist $ U$ ein Unterraum von $ V=\mathbb{R}^2$.

    Ferner gilt (entsprechend dem Lösungsverfahren für lineare Gleichungssysteme)

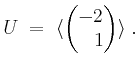
    $\displaystyle U \;=\; \langle\begin{pmatrix}-2 \\ \hfill 1\end{pmatrix}\rangle\;. $

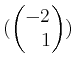    Also wird $ U$ vom Tupel $ (\begin{pmatrix}-2 \\ \phantom{-}1\end{pmatrix})$ (von Länge 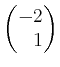$ 1$) erzeugt. Da $ \begin{pmatrix}-2 \\ \phantom{-}1\end{pmatrix}$ ungleich dem Nullvektor ist, ist dieses Tupel auch linear unabhängig und bildet daher eine Basis von $ U$. Es ist $ \dim U=1$.

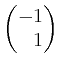  2. Die Vektoren $ \begin{pmatrix}1 \\ 1\end{pmatrix}$ und $ \begin{pmatrix}-1 \\ \phantom{-}1\end{pmatrix}$ liegen beide in $ U$, nicht aber deren Summe

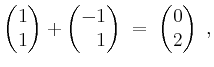
    $\displaystyle \begin{pmatrix}1 \\ 1\end{pmatrix} + \begin{pmatrix}-1 \\ \phantom{-}1\end{pmatrix} \;=\; \begin{pmatrix}0 \\ 2\end{pmatrix}\;, $

    denn es ist $ 0^2\ne 2^2$. Daher ist $ U$ kein Unterraum.

  3. Das Nullpolynom 0 liegt in $ U$. Sind ferner $ p=\sum_{k=0}^n a_k X^k$ und $ q=\sum_{k=0}^n b_k X^k$ Elemente von $ U$, und sind $ \lambda,\,\mu\,\in\, K$, so ist

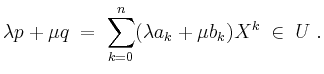
    $\displaystyle \lambda p + \mu q \;=\; \sum_{k=0}^n (\lambda a_k + \mu b_k)X^k \;\in\; U\;. $

    Also ist $ U$ ein Unterraum von $ V=K[X]$.

    Nach der Definition der Polynome ist das Tupel der Monome $ (X^0, X^1 , \dots , X^n)$ linear unabhängig, denn eine Linearkombination davon kann nur das Nullpolynom ergeben, wenn alle ihre Koeffizienten verschwinden.

    Da es auch erzeugend ist, bildet $ (X^0, X^1 , \dots , X^n)$ eine Basis von $ U=K[X]_{\leq n}$, und es ist $ \dim U=n+1$.

  4. Das Nullpolynom $ p=0$ erfüllt $ p(0)=0$ und $ p(1) = 0$, d.h. es gilt $ 0\in U$. Seien ferner $ p,q\in U$ beliebig, d.h. es gelte $ p(0) = q(0) = p(1) = q(1) = 0$, und seien $ \lambda,\mu\in K$. Für das Einsetzen von Werten $ a\in K$ in Polynome gilt die leicht nachzuprüfende Regel

    $\displaystyle (\lambda p + \mu q)(a) \;=\; \lambda p(a) + \mu q(a) \;. $

    Es werden daher

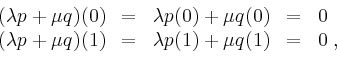
    \begin{displaymath} \begin{array}{rclcl} (\lambda p+\mu q)(0) & = & \lambda p(0)... ...q)(1) & = & \lambda p(1) + \mu q(1) & = & 0 \; ,\\ \end{array}\end{displaymath}

    und somit ist $ \lambda p+\mu q\in U$. Folglich ist $ U$ ein Unterraum von $ V=K[X]_{\leq n}$.

    Wegen $ p(0)=a_0$ und $ p(1) = \sum_{k = 0}^n a_k$ für $ p=\sum_{k=0}^n a_k X^k$ folgt

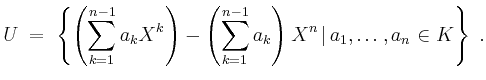
    $\displaystyle U \;=\; \left\{\left(\sum_{k=1}^{n-1} a_k X^k\right) - \left(\sum_{k=1}^{n-1} a_k\right)X^n\,\vert\, a_1,\dots,a_n\in K\right\}\;. $

    Also wird $ U$ erzeugt von $ (X^1 - X^n,X^2 - X^n\dots,X^{n-1} - X^n)$, und dieses Tupel bildet wegen seiner linearen Unabhängigkeit auch eine Basis von $ U$. Es wird $ \dim U = n-1$.

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Verweise]
  automatisch erstellt am 16.  2. 2011