Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Extrema mit Nebenbedingungen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Sei $ n\ge 2$ , und sei $ f:\mathbb{R}^n \to \mathbb{R}$ definiert durch $ f(x_1, \ldots, x_n) := x_1^2 \cdot \ldots \cdot x_n^2$ .

Untersuche die Einschränkung von $ f$ auf die offene Menge $ M := \{ x\in\mathbb{R}^n\; \vert\; f(x)\ne 0\}$ auf lokale Extrema unter der Nebenbedingung $ x_1^2 + \cdots + x_n^2 = 1$ .

Beachte ferner, daß aus Symmetriegründen aus jeder lokalen Maximalstelle $ (x_1,\dots,x_n)^\mathrm{t}$ die lokalen Maximalstellen $ (\pm x_1,\dots,\pm x_n)^\mathrm{t}$ folgen, und genauso für eventuelle Minimalstellen.

Lösung.

Wir setzen $ g:M \to \mathbb{R}, \; (x_1, \ldots, x_n)^\mathrm{t} \mapsto x_1^2 + \cdots + x_n^2 -1$ . Da $ M\subseteq\mathbb{R}^n$ offen ist und $ f$ und $ g$ beliebig oft stetig differenzierbar sind, untersuchen wir mittels der Multiplikatorenregel von Lagrange auf lokale Extrema von $ f$ unter der Nebenbedingung $ g=0$ .

Notwendige Bedingung.

Betrachte die Funktion

$\displaystyle F\; :\; \mathbb{R}^n \;\to\; \mathbb{R}\; , \;\;\; (x_1, \ldots, ... ..., x_n) \;=\; x_1^2 \cdots x_n^2 - \lambda ( x_1^2 + \cdots + x_n^2 - 1 ) \; . $

Es ist

$\displaystyle F'(x) = \begin{pmatrix} \; 2 x_1 x_2^2 \cdots x_n^2 - 2 \lambda ... ...ldots\; , & 2 x_n x_1^2 \cdots x_{n-1}^2 - 2 \lambda x_n\; \end{pmatrix}\; . $

Wäre $ x_k = 0$ für ein $ k\in \{ 1, \ldots, n\}$ , so hätten wir $ f(x) = 0$ , und also $ x\not\in M$ , was uns gemäß Aufgabenstellung nicht interessiert.

Aus der notwendigen Bedingung für Extrema von $ F$ erhalten wir die Gleichungen

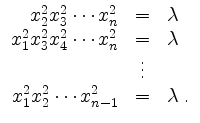
$\displaystyle \begin{array}{rcl} x_2^2 x_3^2 \cdots x_n^2 & = & \lambda\\ x_1^... ... & \vdots &\\ x_1^2 x_2^2 \cdots x_{n-1}^2 & = & \lambda \; . \\ \end{array}$

Folglich sind die linken Seiten alle gleich. Kürzen von Faktoren beim Gleichsetzen je zweier dieser linken Seiten liefert $ x_1^2 = \cdots = x_n^2$ .

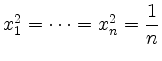Mit der Nebenbedingung $ g=0$ ergibt sich damit $ x_1^2 + \cdots + x_n^2 = n x_1^2 = 1$ , und also $ x_1^2 = \cdots = x_n^2 = \dfrac{1}{n}$ .

Insgesamt sind die $ 2^n$ Punkte $ (\varepsilon_1 n^{-1/2}, \ldots, \varepsilon_n n^{-1/2})^\mathrm{t}$ , mit $ \varepsilon_k\in\{ -1, +1\}$ für alle $ 1\le k\le n$ , kritische Punkte, und wegen $ g'(x) = \begin{pmatrix}\; 2x_1\;, & \cdots\; , & 2x_n\; \end{pmatrix}$ auch allesamt regulär - $ g'$ hat an diesen Stellen Rang $ 1$ .

Hinreichende Bedingung.

Wie in der Aufgabenstellung erwähnt, genügt die Untersuchung von $ x_0 := (n^{-1/2},\dots,n^{-1/2})$ . Wir behaupten, daß an dieser Stelle, und damit an allen regulären kritischen Punkten, ein lokales Maximum unter Nebenbedingung $ g=0$ vorliegt. Halten wir fest, daß dort $ \lambda = n^{1-n}$ ist.

Wir berechnen die relative Hessematrix $ \mathrm{H}_{f;g}(x_0)$ .

Zunächst ist

\begin{displaymath} \mathrm{H}_{F}(x_0) \;=\; 2 n^{1-n} \left[ \begin{array}{ccc... ... 0 \\ \end{array}\right] \; \in\; \mathbb{R}^{n\times n}\; . \end{displaymath}

Wegen $ g'(x_0) = 2n^{-1/2}(\, 1\, ,\; 1\, , \;\dots\; ,\; 1\, )$ können wir

\begin{displaymath} \mathrm{T}_g(x_0) \;=\;\left[ \begin{array}{cccc} 1 & 0 &\c... ...& -1 \\ \end{array}\right] \;\in\; \mathbb{R}^{n\times (n-1)} \end{displaymath}

wählen und erhalten

\begin{displaymath} \mathrm{H}_{f;g}(x_0) \;=\; \mathrm{T}_g(x_0)^\mathrm{t}\,\m... ... \end{array}\right]\; \in\; \mathbb{R}^{(n-1)\times (n-1)}\; . \end{displaymath}

Die Eigenwerte von $ \mathrm{H}_{f;g}(x_0)$ sind $ - 4 n^{1-n}\cdot 1$ (mit Multiplizität $ n-2$ ) und $ - 4 n^{1-n}\cdot n$ (mit Multiplizität $ 1$ ). Folglich ist $ \mathrm{H}_{f;g}(x_0)$ negativ definit, und es liegt bei $ x_0$ in der Tat ein lokales Maximum unter Nebenbedingung $ g=0$ vor.

Der Maximalwert beträgt dort $ f(x_0) = n^{-n}$ .

Skizze des Graphen von $ f\vert _{V(g)}$ im Falle $ n = 2$ .

\includegraphics[width = 8cm]{l3.eps}
(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 11.  8. 2006