Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Oberfläche einer Kugel

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Berechne die Oberfläche einer Kugel mit Radius $ r$ . Verwende dabei die Parametrisierung

$\displaystyle \Phi:[0,\pi]\times[-\pi,\pi]\to\mathbb{R}^3,\; (\psi,\varphi)^\m... ...sin\psi)(\cos\varphi)\\ r(\sin\psi)(\sin\varphi)\\ r\cos\psi \end{pmatrix}\;. $

Lösung.

Wir berechnen zunächst den Normalenvektor der Fläche $ \Phi$ durch

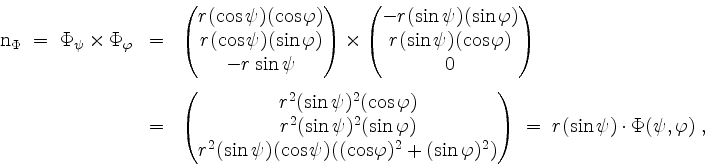
\begin{displaymath} \begin{array}{rcl} \mathrm{n}_{\Phi} \;=\; \Phi_\psi\times\P... ...pmatrix}\;=\; r(\sin\psi)\cdot\Phi(\psi,\varphi)\;, \end{array}\end{displaymath}

was der Anschauuung entspricht, daß der Vektor vom Ursprung zu einem Punkt auf der Kugel normal zur Kugeloberfläche steht.

Also errechnet sich der Flächeninhalt der Kugel unter Beachtung von $ \Vert\Phi(\psi,\varphi)\Vert=r$ zu

\begin{displaymath} \begin{array}{rcl} \mathrm{area}(\Phi) &=& \displaystyle\int... ...os\psi\right]_0^\pi\vspace*{4mm}\\ &=& 4\pi r^2\;. \end{array}\end{displaymath}

Der Flächeninhalt des Kreises mit Radius $ r$ ist $ \pi r^2$ , ihr Umfang ist davon die Ableitung nach $ r$ , nämlich $ 2\pi r$ .

Das Volumen der Kugel mit Radius $ r$ ist $ 4\pi r^3/3$ , ihre Oberfläche ist, wie eben gesehen, davon die Ableitung nach $ r$ , nämlich $ 4\pi r^2$ .

Warum?

(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 11.  8. 2006