Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Mensa

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Auf dem Speiseplan einer Mensa stehen Fisch und Eintopf. Der Koch soll die Gesamteinnahmen maximieren und muss dabei folgendes berücksichtigen. Um das Problem in Standardform zu bringen, ersetzt man die Nebenbedingung "(Anzahl der Gerichte)$ \leq 1000$" durch "$ -$(Anzahl der Gerichte)$ \geq 1000$". Mit $ x$ den Portionen Fisch und $ y$ den Portionen Eintopf erhält man das Problem

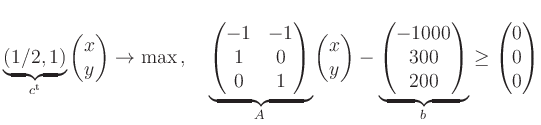
$\displaystyle \underbrace{(1/2,1)}_{c^{\operatorname{t}}}\begin{pmatrix}x \\ y\... ...00 \\ 300\\ 200\end{pmatrix}}_{b} \geq \begin{pmatrix}0 \\ 0\\ 0\end{pmatrix} $

Es existieren also Lagrange-Muliplikatoren $ \lambda, \sigma, \rho \le 0$ mit

$\displaystyle \frac{1}{2}$ $\displaystyle =$ $\displaystyle - \lambda + \sigma$  
$\displaystyle 1$ $\displaystyle =$ $\displaystyle - \lambda+\rho$  
$\displaystyle \lambda (x_*+y_* - 1000)$ $\displaystyle =$ 0  
$\displaystyle \sigma (x_* - 300)$ $\displaystyle =$ 0  
$\displaystyle \rho (y_* - 200)$ $\displaystyle =$ 0  

$ \lambda = 0$ führt zu $ \rho = 1$, also einem Widerspruch. Damit ist $ x_* + y_* = 1000$.

$ \sigma = 0$ führt zu $ \lambda = -\frac{1}{2}, \rho = \frac{1}{2}$, also auch zu einem Widerspruch. Somit ist $ x_* = 300$.

Folglich erhält man als Lösung:

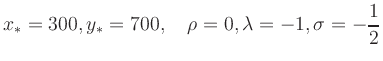
$\displaystyle x_* = 300, y_* = 700,\quad \rho = 0, \lambda =- 1, \sigma = -\frac{1}{2}$

Der Koch sollte also 300 Portionen Fisch und 700 Portionen Eintopf kochen.

Die Lösung kann man in diesem einfachen Beispiel auch grafisch konstruieren.

\includegraphics[width=0.5\linewidth]{Bild_Beispiel_Mensa}

Zur Bestimmung der optimalen Ecke $ (x_*,y_*)$ verschiebt man die Niveaugerade der Zielfunktion (gestrichelt) so lange in Richtung des Gradienten $ c$ bis sie den grauen zulässigen Bereich nicht mehr schneidet.

[Verweise]
  automatisch erstellt am 26.  1. 2017