Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Lösung einer elliptischen PDG mit dem Separationsansatz

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Wir geben ein weiteres Beispiel zur Separationsmethode.

Beispiel: Gegeben sei die elliptische PDG $ (\Delta > 0)$

$\displaystyle u_{xx} + u_{yy} - 2u_y + au = 0 , \ \ \ \ a \in \mathbb{R} .$

Der Ansatz

$\displaystyle u(x,y) = v(x) \cdot w(y) $

ergibt

$\displaystyle v''w + vw'' - 2vw' + avw = 0 .$

Die triviale Lösung $ u = 0$ klammern wir aus und können daher $ v \neq 0$ bzw. $ w \neq 0$ annehmen. Divison mit $ vw$ ergibt

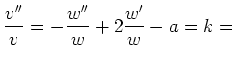$\displaystyle \frac{v''}{v} = - \frac{w''}{w} + 2 \frac{w'}{w} - a = k =$    const.

Wir nehmen an, daß die Randbedingungen $ u(0,y) = u(\pi,y) = u(\frac{\pi}{2},y) = 0$ vorgegeben seien.

Falls $ k = 0 ,$ dann ist $ v(x) = c_1x +c_2 .$ Man sieht unmittelbar, daß in diesem Fall die Randbedingungen nur trivial erfüllbar sind.

Falls $ k > 0 ,$ dann ist $ v(x) = c_1 e^{\sqrt{k}x} + c_2 e^{-\sqrt{k}x} .$ Auch in diesem Fall sind die Randbedingungen nur trivial erfüllbar.

Falls $ k < 0 ,$ dann ist $ v(x) = c_1 \cos \sqrt{-k}x + c_2 \sin \sqrt{-k}x .$ $ v(0) = 0 \longrightarrow c_1 = 0 , v(\frac{\pi}{2}) = 0 \longrightarrow \sin (\sqrt{-k} \frac{\pi}{2}) = 0 .$ Daher ist $ k = - 4n^2 $ mit $ n \in \mathbb{N} .$ Die Bedingung $ v(\pi) = 0$ ist dann automatisch erfüllt.

Somit kann nur $ v (x) = c_2 \sin 2nx , \ n\in \mathbb{N} ,$ zu nichttrivialen Lösungen der PDG führen.

Für $ w = w(y)$ ist noch die Differentialgleichung

$\displaystyle w'' - 2w' + (a - 4n^2) w = 0 $

im Fall $ k = - 4n^2 $ zu lösen, also eine gewöhnliche DGL mit konstanten Koeffizienten. Der Ansatz $ w = e^{\lambda y}$ liefert

$\displaystyle \lambda^2 - 2 \lambda + (a - 4n^2) =0.$

Ist etwa $ a =1 ,$ dann folgt $ \lambda = 1 \pm 2n .$ Also ist mit Konstanten $ d_1, d_2 \in \mathbb{R} $

$\displaystyle w(y) = d_1 e^{(1+2n)y} + d_2 e^{(1-2n)y} \ , \ \ \ n \in \mathbb{N}$

und

$\displaystyle u(x,y) = (c_2 \sin 2nx)(d_1 e^{(1+2n)y} + d_2 e^{(1-2n)y}) \ , \ \ n \in \mathbb{N} .$

Durch Stellen von Anfangsbedingungen können sich weitere Einschränkungen an $ c_2, d_1, d_2 $ ergeben.

(Aus: Vorlesungsskript HM3)
[Verweise]
  automatisch erstellt am 25.  1. 2006