
Mathematik-Online-Lexikon: Erläuterung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: Erläuterung zu | |
Additionstheoreme von Sinus und Cosinus |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Für die Kreisfunktionen ![]() und
und ![]() gelten folgende
Beziehungen:
gelten folgende
Beziehungen:
Insbesondere ist
(i) Elementargeometrischer Beweis:
Für
![]() wird die folgende Konstruktion
betrachtet.
wird die folgende Konstruktion
betrachtet.
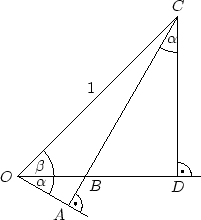
Im Dreieck
![]() gilt
gilt


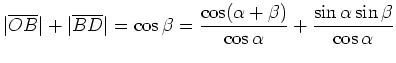
Analog argumentiert man für andere Winkelbereiche ![]() oder
oder
![]() und erhält so das Additionstheorem für den
Cosinus.
und erhält so das Additionstheorem für den
Cosinus.
Das Additionstheorem des Sinus folgt hieraus mit den Beziehungen
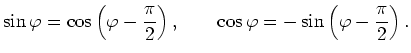

(ii) Beweis mit Hilfe der Differentialrechnung:
Man setzt zunächst
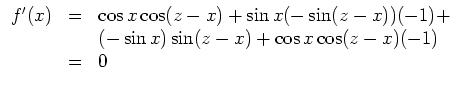
(iii) Beweis mit der Formel von Euler-Moivre:
Mit der Formel von Euler-Moivre kann man die Exponentialfunktion auch für komplexe Zahlen definieren:
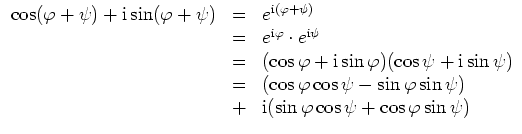
| automatisch erstellt am 25. 1. 2006 |