Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Existenz eines Potentials

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Für ein stetiges Vektorfeld $ \vec{F}$ auf einem zusammenhängenden Gebiet $ D$ existiert ein Potential $ U$ genau dann, wenn das Arbeitsintegral wegunabhängig ist. In diesem Fall ist

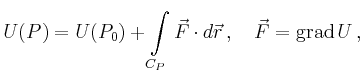
$\displaystyle U(P) = U(P_0)+ \int\limits_{C_P} \vec{F} \cdot d\vec{r}\,, \quad \vec{F} = \operatorname{grad} U \,, $

wobei $ {C_P}: t\mapsto \vec{r}(t)$ ein beliebiger in $ D$ verlaufender Weg ist, der einen fest gewählten Punkt $ P_0\in D$ mit $ P$ verbindet. Insbesondere ist $ U$ bis auf eine Konstante (den Wert $ U(P_0)$) eindeutig bestimmt.

Ist $ \vec{F}$ stetig differenzierbar auf einer offenen Menge $ D$ ist

$\displaystyle \operatorname{rot} \vec{F} =0 $

notwendig für die Existenz eines Potentials. Ist $ D$ einfach zusammenhängend, so ist die Wirbelfreiheit ebenfalls hinreichend.

Die Wegunabhängigkeit ist notwendig, da

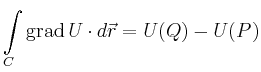
$\displaystyle \int\limits_{C} \operatorname{grad}U\cdot d\vec{r} = U(Q)-U(P) $

für jeden die Punkte $ P$ und $ Q$ verbindenden Weg $ C$ gilt.

Dass die Wegunabhängigkeit hinreichend ist, ergibt sich aus folgender Überlegung:

Da $ D$ offen ist, gibt es zu einem Punkt $ P$ einen Wert $ h>0$, so dass für $ \vec{q}=\vec{p}+h\vec{e}_i$ die gesamte Strecke $ S=\overline{PQ}$ in $ D$ enthalten ist.

\includegraphics[width=.5\linewidth]{e_potential_existenz_bild}

Aufgrund der Wegunabhängigkeit des Arbeitsintegrals kann man nun für den Wert $ U(Q)$ den Weg $ C_P$ zu $ P$ um die Strecke $ S$ ergänzen. Dann ergibt sich für die Potentialdifferenz

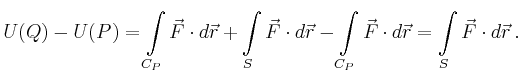
$\displaystyle U(Q)-U(P) = \int\limits_{C_P} \vec{F}\cdot d\vec{r} + \int\limit... ...nt\limits_{C_P} \vec{F}\cdot d\vec{r} =\int\limits_S \vec{F} \cdot d\vec{r}\,. $

Mit der Parametrisierung

$\displaystyle S: \vec{r}(t) = \vec{p}+t\vec{e}_i\,,\quad t \in [0,h]\,, $

ist

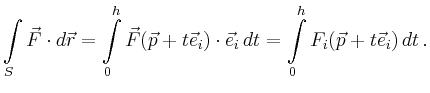
$\displaystyle \int\limits_S \vec{F} \cdot d\vec{r} = \int\limits_0^h \vec{F}(\v... ...ec{e}_i)\cdot \vec{e}_i\, dt = \int\limits_0^h F_i(\vec{p}+t\vec{e}_i)\, dt\,. $

Der Mittelwertsatz der Integralrechnung liefert nun

$\displaystyle \int\limits_0^h F_i(\vec{p}+t\vec{e}_i) dt = hF_i(\vec{p}+\tau \vec{e}_i)\,,\quad \tau \in[0,h]\,. $

Für die $ i$-te Komponente des Gradienten folgt also

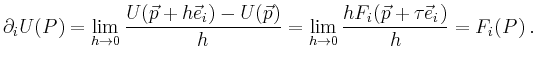
$\displaystyle \partial_i U (P)= \lim\limits_{h\to 0} \frac{U(\vec{p}+h\vec{e}_i... ...)}{h} =\lim\limits_{h\to 0} \frac{hF_i(\vec{p}+\tau \vec{e}_i)}{h} = F_i(P)\,. $

Somit ist $ U$ tatsächlich ein Potential für $ \vec{F}$.

Für stetig differenzierbare Vektorfelder folgt die Notwendigkeit der Wirbelfreiheit unmittelbar aus der Vertauschbarkeit der partiellen Ableitungen. Ist $ \vec{F}=\operatorname{grad}U$, so folgt

$\displaystyle \partial_iF_j-\partial_jF_i= \partial_i\partial_j U - \partial_j\partial_i U = 0\,. $

Ist $ D$ einfach zusammenhängend, so berandet jede geschlossene Kurve $ C$ eine Fläche $ S$ in $ D$. Der Satz von Stokes,

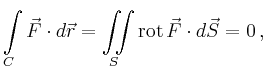
$\displaystyle \int\limits_C \vec{F}\cdot d\vec{r} = \iint\limits_S \operatorname{rot} \vec{F}\cdot d\vec{S} =0\,, $

impliziert damit die Wegunabhängigkeit.
[Zurück]
  automatisch erstellt am 9. 10. 2013