Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1132: Kern einer linearen Abbildung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

In Abhängigkeit von dem Parameter $ t\in\mathbb{R}$ ist die folgende Matrix

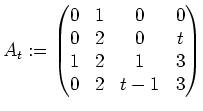
$\displaystyle A_t:=\left(\begin{matrix} 0 & 1 & 0 & 0 \\ 0 & 2 & 0 & t \\ 1 & 2 & 1 & 3 \\ 0 & 2 & t-1 & 3 \\ \end{matrix}\right) $

gegeben, die die lineare Abbildung $ \alpha_t\colon\mathbb{R}^4\rightarrow\mathbb{R}^4\colon x\mapsto A_tx$ beschreibt.

Bestimmen Sie in Abhängigkeit von $ t$ $ \mathrm{Kern}(\alpha_t)$.

Hinweis: Es kann hierbei im Gauß-Algorithmus nötig sein, Spalten zu vertauschen.

Zur Bestimmung des Kerns müssen wir das homogene Gleichungssystem $ A\vec{x}=0$ lösen. Wir starten mit der Matrix

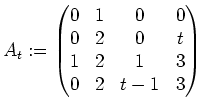$\displaystyle A_t:=\left(\begin{matrix}0 & 1 & 0 & 0 \\ 0 & 2 & 0 & t \\ 1 & 2 & 1 & 3 \\ 0 & 2 & t-1 & 3 \\ \end{matrix}\right)$    

Durch Zeilenumformungen bringen wir sie auf die Gestalt

$\displaystyle \begin{pmatrix}1 & 0 & 1 & 3 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & t-1& 3 \\ 0 & 0 & 0 & t \end{pmatrix}$    

Aus dieser Matrix können wir ablesen, dass wir drei Fälle unterscheiden müssen. Zum einen den Fall, in welchem $ t\neq 1$ und $ t\neq 0$. Dann hat die Matrix vollen Rang und nach dem Dimensionssatz hat der Kern dann Dimension 0, d.h. $ \operatorname{Kern}{A_t}=\{0\}$.

Angenommen, es ist $ t=0$. Dann hat die Matrix die Form:

$\displaystyle \begin{pmatrix}1 & 0 & 1 & 3 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1& 3 \\ 0 & 0 & 0 & 0 \end{pmatrix}$    

Durch den restlichen Gaussalgorithmus erhalten wir als Lösung des LGS und damit als Kern:

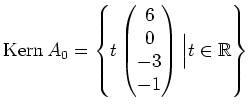$\displaystyle \operatorname{Kern}{A_0}=\left\{t\begin{pmatrix}6 \\ 0 \\ -3 \\ -1 \end{pmatrix}\Big\vert t\in\mathbb{R}\right\}$    

Angenommen, es ist $ t=1$. Dann hat die Matrix die Form:

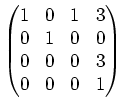$\displaystyle \begin{pmatrix}1 & 0 & 1 & 3 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 1 \end{pmatrix}$    

Wir vertauschen die 3. und 4. Spalte und anschliessend bringen wir den Gaussalgorithmus zu Ende. Dies ergibt die Matrix:

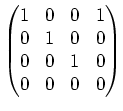$\displaystyle \begin{pmatrix}1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}$    

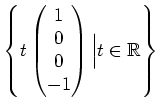Abgelesen ergäbe das die Lösungsmenge $ \left\{t\begin{pmatrix}1\\ 0\\ 0\\ -1\end{pmatrix}\Big\vert t\in\mathbb{R}\right\}$. Wegen der Spaltenvertauschung müssen wir aber noch die 3. und 4. Zeile der Lösung zurücktauschen und erhalten:

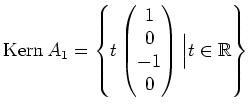$\displaystyle \operatorname{Kern}{A_1}=\left\{t\begin{pmatrix}1\\ 0\\ -1\\ 0\end{pmatrix}\Big\vert t\in\mathbb{R}\right\}$    

(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 19. 12. 2005