Mathematik-Online-Aufgabensammlung: Lösung zu: Aufgabe 1342: Möndchen des Hippokrates

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Aufgabensammlung: Lösung zu
	Aufgabe 1342: Möndchen des Hippokrates

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Sei . Bestimmen Sie den Flächeninhalt des Möndchen des Hippokrates

$\displaystyle M:\quad x^2+y^2 \leq r^2\,,\quad (x+r)^2 + y^2 \geq 2r^2\,.$

$\includegraphics[width=0.6\linewidth]{Hippokratesmoendchen.eps}$

Zunächst betrachten wir den Schnitt $M^y=\{x\in\mathbb{R}\ \vert\ (x,y)^\mathrm{t}\in M\}$ . Diese Menge ist leer, falls $\vert y\vert>r$ ist. Für $\vert y\vert\leq r$ erhalten wir die Bedingungen

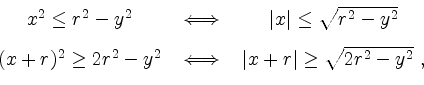
$\begin{displaymath} \begin{array}{ccc} x^2\leq r^2-y^2&\iff&\vert x\vert\leq\sqr... ... 2r^2-y^2&\iff&\vert x+r\vert\geq\sqrt{2r^2-y^2}\ , \end{array}\end{displaymath}$

also

$\displaystyle -r+\sqrt{2r^2-y^2}\;\le\; x\;\le\; \sqrt{r^2-y^2}\; ,$

und somit

$\begin{displaymath} M^y\; =\; \begin{cases} \emptyset & \mbox{f''ur $\vert y\ve... ...^2-y^2}] & \mbox{f''ur $\vert y\vert\leq r$}\; .\\ \end{cases}\end{displaymath}$

Also ist

$\displaystyle M'\; =\;\{y\in\mathbb{R}\; \vert\; M^y\neq\emptyset\} \; =\; [-r,r]\; .$

Wir berechnen

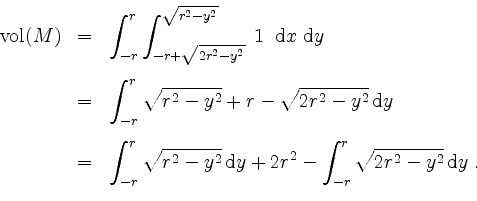
$\begin{displaymath} \begin{array}{rcl} \mathrm{vol}(M) & = & \displaystyle\int_{... ...- \int_{-r}^r \sqrt{2r^2-y^2}\,\mathrm{d}y \; . \\ \end{array}\end{displaymath}$

Eine Nebenrechnung mit partieller Integration gibt

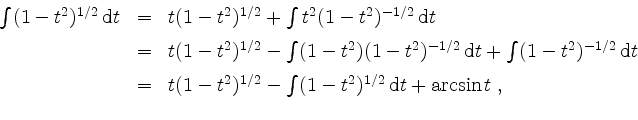
$\begin{displaymath} \begin{array}{rcl} \int (1-t^2)^{1/2}\,\mathrm{d} t & = & t ... ...{1/2}\,\mathrm{d} t + \arcsin t\; , \vspace{2mm}\\ \end{array}\end{displaymath}$

und somit

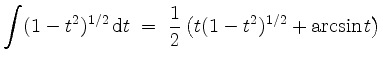
$\displaystyle \int (1-t^2)^{1/2}\,\mathrm{d} t \;=\; \frac{1}{2}\left( t(1-t^2)^{1/2} + \arcsin t\right)$

Wir können fortfahren mit

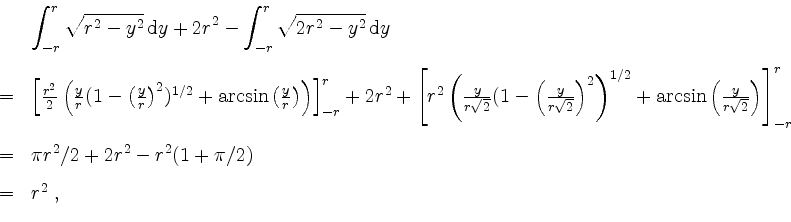
$\begin{displaymath} \begin{array}{cl} & \displaystyle\int_{-r}^r \sqrt{r^2-y^2}... ...pi/2) \vspace{3mm} \\ = & r^2\; , \vspace{3mm} \\ \end{array}\end{displaymath}$

d.h. $\mathrm{vol}(M) = r^2$ .

Es ist eine gute Probe, das Ergebnis mit der Anschauung zu vergleichen, vgl. Aufgabenstellung.

Außerdem, wenn eine Figur in $\mathbb{R}^n$ von einem Parameter zentral gestreckt wird, wie etwa im vorliegenden Fall, so ist ihr Inhalt proportional zu .

(Autoren: Künzer/Martin/Tentler/Wahrheit)

[Zurück zur Aufgabe]

automatisch erstellt am 11. 8. 2006