
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1344: Volumen und Integral eines Ellipsoids |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Seien
![]() . Bestimme das Volumen des Ellipsoids
. Bestimme das Volumen des Ellipsoids
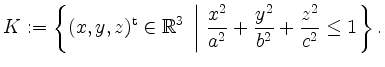
Berechne ferner ![]() für
für
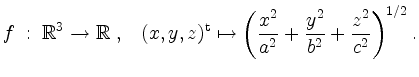
Wir verwenden die verallgemeinerte Kugelkoordinatentransformation
und erhalten
Wir berechnen zunächst

Damit berechnet sich das Volumen des Ellipsoiden zu

Schließlich ist

Der Dimensionstest ist in Ordnung, da der Wert von ![]() die Dimension 0
hatte.
die Dimension 0
hatte.
| automatisch erstellt am 11. 8. 2006 |