Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Vektoranalysis - Integration - Integralsätze von Green und Stokes

Satz von Stokes

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Ist $ \vec{F}$ ein stetig differenzierbares Vektorfeld auf einer regulären Fläche $ S$ mit orientiertem Rand $ C$, so gilt

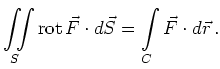
$\displaystyle \iint\limits_S \operatorname{rot} \vec{F} \cdot d\vec{S} = \int\limits_C \vec{F} \cdot d\vec{r}\,. $

Die Glattheitsvoraussetzungen an $ \vec{F}$ und $ S$ können abgeschwächt werden, indem man die Integrale über geeignete Grenzprozesse definiert.

Als Beispiel wird der Fluss der Rotation des räumlichen Vektorfeldes

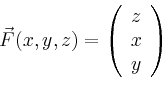
\begin{displaymath} \vec{F}(x,y,z)=\left( \begin{array}{c} z\\ x\\ y\\ \end{array}\right) \end{displaymath}

durch die Halbkugelschale

$\displaystyle S:\quad x^2+y^2+z^2=1,\quad z\geq 0\,, $

betrachtet. Als Parametrisierung für die Randkurve $ C$ wird

\begin{displaymath} \vec{r}(t)=\left( \begin{array}{c} \cos t\\ \sin t \\ 0\\ \end{array}\right),\quad t\in[0,2\pi]\,, \end{displaymath}

mit

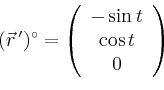
\begin{displaymath} (\vec{r}\,')^\circ =\left( \begin{array}{c} -\sin t\\ \cos t \\ 0\\ \end{array}\right) \end{displaymath}

verwendet. Mit der Parametrisierung

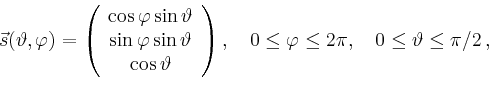
\begin{displaymath} \vec{s}(\vartheta,\varphi)=\left( \begin{array}{c} \cos\varp... ...,\quad 0\leq\varphi\leq 2\pi,\quad 0\leq\vartheta\leq \pi/2\,, \end{displaymath}

für die Halbkugelschale ergibt sich

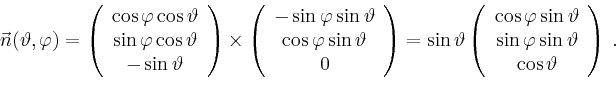
\begin{displaymath} \vec{n}(\vartheta,\varphi)= \left( \begin{array}{c} \cos\var... ...\varphi\sin\vartheta\\ \cos\vartheta\\ \end{array}\right)\,. \end{displaymath}

Für die Rotation von $ \vec{F}$ gilt

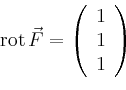
\begin{displaymath} \operatorname{rot}\vec{F} = \left( \begin{array}{c} 1\\ 1\\ 1\\ \end{array}\right) \end{displaymath}

und somit für die linke Seite im Satz von Stokes

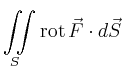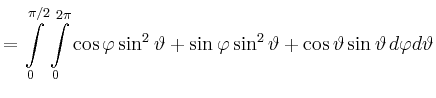$\displaystyle \iint\limits_{S} \operatorname{rot} \vec{F} \cdot d\vec{S}$ $\displaystyle = \int\limits_0^{\pi/2}\int\limits_0^{2\pi} \cos\varphi\sin^2\var... ... + \sin\varphi\sin^2\vartheta + \cos\vartheta\sin\vartheta\,d\varphi d\vartheta$    
  $\displaystyle = 0+0+2\pi\left[\frac{1}{2}\sin^2\vartheta\right]_{\vartheta=0}^{\pi/2}=\pi\,.$    

Für die rechte Seite erhält man entsprechend

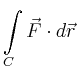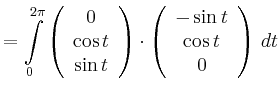$\displaystyle \int\limits_{C} \vec{F} \cdot d\vec{r}$ $\displaystyle = \int\limits_0^{2\pi} \left( \begin{array}{c} 0\\ \cos t \\ \sin... ...ht)\cdot \left( \begin{array}{c} -\sin t\\ \cos t \\ 0\\ \end{array}\right)\,dt$    
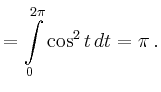  $\displaystyle = \int\limits_0^{2\pi} \cos^2 t\,dt = \pi\,.$    

Betrachtet man statt der Halbkugelschale die Kreisscheibe

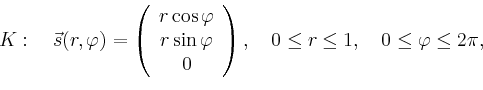
\begin{displaymath} K:\quad\vec{s}(r,\varphi)=\left( \begin{array}{c} r\cos\varp... ...{array}\right),\quad 0\leq r\leq1,\quad 0\leq\varphi\leq 2\pi, \end{displaymath}

mit gleichem Rand $ C$, so bleibt die rechte Seite unverändert, während sich für die linke in Polarkoordinaten ebenfalls

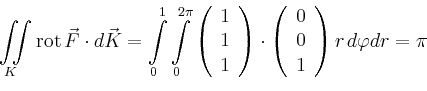
\begin{displaymath} \iint\limits_{K} \operatorname{rot} \vec{F} \cdot d\vec{K} =... ...array}{c} 0\\ 0\\ 1\\ \end{array}\right) r\,d\varphi dr = \pi \end{displaymath}

ergibt.
Als Beispiel wird der Fluss der Rotation des räumlichen Vektorfeldes

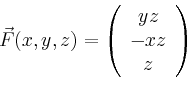
\begin{displaymath} \vec{F}(x,y,z)=\left( \begin{array}{c} yz\\ -xz\\ z\\ \end{array}\right) \end{displaymath}

nach außen durch den Zylindermantel

$\displaystyle S:\quad x^2+y^2 = 1,\quad 0\leq z \leq 1\,, $

betrachtet. Als Parametrisierung für die untere Randkurve $ C_u$ wird

\begin{displaymath} \vec{r}(t)=\left( \begin{array}{c} \cos t\\ \sin t \\ 0\\ \end{array}\right),\quad t\in[0,2\pi]\,, \end{displaymath}

verwendet. Entsprechend ist für die obere Randkurve $ C_o$

\begin{displaymath} \vec{r}(t)=\left( \begin{array}{c} \cos(-t)\\ \sin(-t) \\ 1\\ \end{array}\right),\quad t\in[0,2\pi]\,, \end{displaymath}

wobei die entgegengesetzte Orientierung zu berücksichtigen ist.

Der gesuchte Fluss ist nach dem Satz von Stokes gleich der Summe der Arbeitsintegrale über die beiden Randkurven,

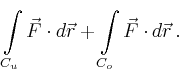
$\displaystyle \int\limits_{C_u} \vec{F} \cdot d\vec{r} + \int\limits_{C_o} \vec{F} \cdot d\vec{r} \,. $

Mit

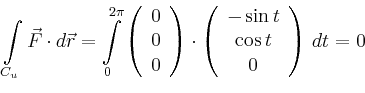
\begin{displaymath} \int\limits_{C_u} \vec{F} \cdot d\vec{r} = \int\limits_0^{... ...n{array}{c} -\sin t\\ \cos t \\ 0\\ \end{array}\right)\,dt =0 \end{displaymath}

und

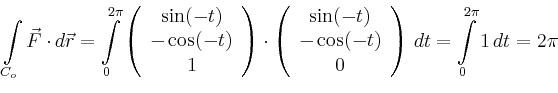
\begin{displaymath} \int\limits_{C_o} \vec{F} \cdot d\vec{r} = \int\limits_0^{... ... \end{array}\right)\,dt = \int\limits_0^{2\pi} 1 \, dt = 2\pi \end{displaymath}

ist der Fluss durch den Mantel also $ 2\pi$.

Alternativ kann der Fluss durch den Mantel auch mit Hilfe der Flüsse durch Deckel und Boden des Zylinders berechnet werden. Da für diese Flächen die Normale parallel zur $ z$-Achse ist, muss nur die $ z$-Komponente der Rotation von $ \vec{F}$ bestimmt werden:

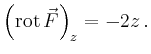
$\displaystyle \left(\operatorname{rot} \vec{F}\right)_z = -2z\,. $

Damit ist der Fluss durch den Boden ($ z=0$) null, und der Fluss durch den Deckel ($ z=1$) entspricht dem $ (-2)$-fachen der Kreisfläche, also $ -2\pi$. Da der Gesamtfluss durch den Zylinder verschwindet ( div rot $ \vec{F} =0$), ist der Fluss durch den Mantel $ 2\pi$.
Eine typische wirbelförmige Strömung um die $ z$-Achse wird durch das Vektorfeld

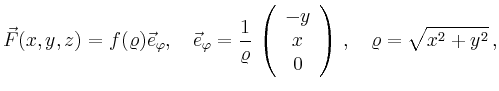
$\displaystyle \vec{F}(x,y,z) = f(\varrho) \vec{e}_\varphi,\quad \vec{e}_\varphi... ...\begin{array}{c}-y\\ x\\ 0\end{array}\right)\, ,\quad\varrho=\sqrt{x^2+y^2}\,, $

beschrieben, wobei

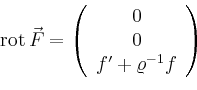
\begin{displaymath} \operatorname{rot} \vec{F} = \left( \begin{array}{c} 0\\ 0\\ f'+\varrho^{-1}f\\ \end{array}\right) \end{displaymath}

nach den Rechenregeln für die Rotation in Zylinderkoordinaten ist.

Gesucht ist nun der Fluss von $ \operatorname{rot} \vec{F} $ durch die Kreisscheibe $ S$ in der $ xy$-Ebene mit Mittelpunkt im Ursprung und Radius $ a>0$. Wählt man als Parametrisierung der Randkurve

\begin{displaymath} C:\quad \vec{r}(t)=\left( \begin{array}{c} a\cos t \\ a\sin ... ...a\sin t \\ a\cos t\\ \end{array}\right),\quad t\in[0,2\pi]\,, \end{displaymath}

so erhält man mit Hilfe des Satzes von Stokes

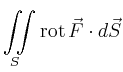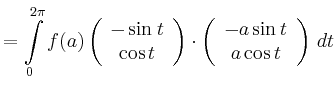$\displaystyle \iint\limits_{S} \operatorname{rot} \vec{F} \cdot d\vec{S}$ $\displaystyle = \int\limits_0^{2\pi} f(a) \left( \begin{array}{c} -\sin t \\ \c... ...right)\cdot\left( \begin{array}{c} -a\sin t \\ a\cos t\\ \end{array}\right)\,dt$    
  $\displaystyle = 2\pi a f(a)\,.$    

Für das Rechteck $ R=[-a,a]\times[-b,b]$ in der $ xy$-Ebene erhält man für den Spezialfall $ f(\varrho)=\varrho$

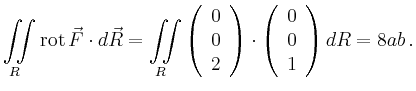
$\displaystyle \iint\limits_R \operatorname{rot} \vec{F} \cdot d\vec{R} = \iint\... ...ay}\right) \cdot \left(\begin{array}{c}0\\ 0\\ 1\end{array}\right) dR = 8ab\,. $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 9.10.2013