Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Komplexe Analysis - Komplexe Integration - Fundamentale Sätze

Cauchysche Integralformel

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Ist $ f$ analytisch in einem Gebiet $ D$ und $ C$ ein geschlossener Weg, der in $ D$ zu einem Punkt homotop ist, dann gilt

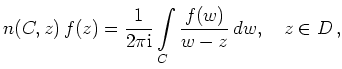
$\displaystyle n(C,z)\,f(z) = \frac{1}{2\pi\mathrm{i}} \int\limits_C \frac{f(w)}{w-z}\,dw, \quad z\in D \,, $

wobei $ n(C,z)$ die Umlaufzahl von $ C$ bezüglich $ z$ ist.

Insbesondere gilt die Formel mit $ n(C,z)=1$ für einen entgegen dem Uhrzeigersinn durchlaufenen Kreis um $ z$.

Die Funktion

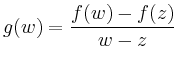
$\displaystyle g(w) = \frac{f(w)-f(z)}{w-z} $

hat lediglich eine schwache Singularität bei $ w=z$:

$\displaystyle \lim_{w\to z}(w-z)g(w) = 0 $

wegen der Stetigkeit von $ f$. Nach Cauchys Theorem ist somit $ \int_C g\,dw = 0$. Es folgt also

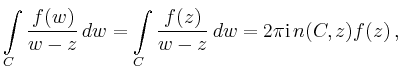
$\displaystyle \int\limits_C \frac{f(w)}{w-z}\,dw = \int\limits_C \frac{f(z)}{w-z}\,dw = 2\pi\mathrm{i}\, n(C,z)f(z) \,, $

wie behauptet.

Als Beispiel wird die Funktion

$\displaystyle f(z)=e^z $

und für $ C$ der entgegen dem Uhrzeigersinn durchlaufene Einheitskreis betrachtet.

Mit Hilfe der Cauchyschen Integralformel erhält man

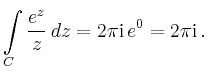
$\displaystyle \int\limits_C \frac{e^z}{z}\,dz = 2\pi\mathrm{i}\,e^0=2\pi\mathrm{i}\,. $

Eine direkte Berechnung mit der Parametrisierung $ z=e^{\mathrm{i}t}$, $ 0\le t\le2\pi$, über das Integral

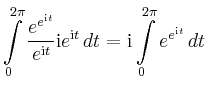
$\displaystyle \int\limits_0^{2\pi} \frac{e^{e^{\mathrm{i}t}}}{e^{\mathrm{i}t}}\... ...{i}e^{\mathrm{i}t}\,dt = \mathrm{i}\int\limits_0^{2\pi}e^{e^{\mathrm{i}t}}\,dt $

führt jedoch nicht zum Erfolg.
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 21.11.2013