Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Integralrechnung - Anwendungen

Länge einer Kurve

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die Länge $ L$ einer Kurve mit stetig differenzierbarer Parametrisierung $ t\mapsto p(t)$ , $ a\le t\le b$ , ist

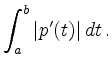
$\displaystyle \int_a^b \vert p^\prime(t)\vert\,dt\, . $

Speziell gilt für eine Kurve in der $ xy$ -Ebene mit der Parameterdarstellung $ p(t)=(x(t),y(t))$

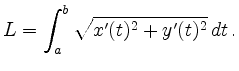
$\displaystyle L = \int_a^b \sqrt{x^\prime(t)^2 + y^\prime(t)^2}\,dt\,. $

Insbesondere hat der Graph einer Funktion $ y=f(x)\,,\,x\in[c,d]$ die Länge

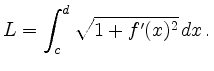
$\displaystyle L = \int_c^d \sqrt{1 + f^\prime(x)^2}\,dx\,. $

Die Länge des Kurvenstücks zwischen $ p(a)$ und $ p(t)$ ,

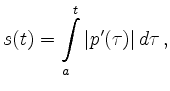
$\displaystyle s(t) = \int\limits_a^t \vert p'(\tau)\vert\,d\tau \,, $

kann als kanonischer Kurvenparameter benutzt werden. Man erhält die sogenannte Parametrisierung nach Bogenlänge:

$\displaystyle q(s) = p(t),\quad\vert q'\vert = 1 \,. $

Aufgrund des normierten Tangentenvektors gilt für diese kanonische Parametrisierung

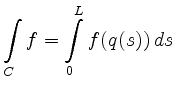
$\displaystyle \int\limits_{C} f = \int\limits_0^{L} f(q(s))\,ds $

mit $ L$ der Länge von $ C$ .

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017