Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Analysis - Extremwerte und Kurvendiskussion

Kurvendiskussion

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Zur Beurteilung des qualitativen Verhaltens einer Funktion können folgende Merkmale herangezogen werden:

\includegraphics[width=0.9\linewidth]{Kurvendiskussion}

Eine entsprechende Analyse der Funktion wird als Funktionsuntersuchung bezeichnet.

Es wird eine Funktionsuntersuchung für die Funktion

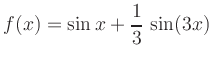
$\displaystyle f(x)=\sin x + \frac{1}{3}\,\sin(3x)$

durchgeführt.

Symmetrie: Da $ \sin x=-\sin(-x)$ ist die Funktion ungerade.

Periodizität: Die Funktion ist wie die Sinusfunktion selbst $ 2\pi$-periodisch und wird im Folgenden daher nur auf dem Intervall $ [-\pi,\pi]$ betrachtet.

Unstetigkeitsstellen und Polstellen: Die Funktion ist aus stetigen Funktionen zusammengesetzt und hat daher keine Unstetigkeitsstellen oder Polstellen.

Nullstellen: Aus dem Additionstheorem folgt $ \sin(3x) = 3\sin x -4\sin^3 x$, und somit ist

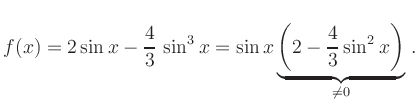
$\displaystyle f(x) = 2 \sin x -\frac{4}{3}\,\sin^3 x = \sin x \underbrace{\left(2-\frac{4}{3}\sin^2 x \right)}_{\neq 0} \,. $

Die Funktion besitzt also Nullstellen bei 0 und $ \pm \pi$.

Extrema: Die Ableitung

$\displaystyle f^\prime(x) = 2 \cos x -4\sin^2 x \,\cos x =-2\cos x +4\cos^3 x $

ist Null für $ \cos x =0$ oder $ \cos x =\pm 1/\sqrt{2}$, also

$\displaystyle x=\pm \pi/2 \quad\lor\quad x=\pm \pi/4 \quad\lor\quad x= \pm 3\pi/4\,. $

Da die Funktion auf ganz $ \mathbb{R}$ definiert und periodisch ist, sind keine Randwerte zu betrachten. Aus dem Vorzeichen der zweiten Ableitung

$\displaystyle f^{\prime\prime}(x) = 2 \sin x -12 \cos^2 x \, \sin x =2 \sin x(1-6\cos^2 x) $

und durch Vergleich der Funktionswerte läßt sich also der Typ der Extrema bestimmen:

\begin{displaymath} \begin{array}{c\vert c\vert c\vert l} x & f(x) & f''(x) & \... ...\sqrt{8}/3 & -2\sqrt{2}<0 & \mbox{globales Maximum} \end{array}\end{displaymath}

Wendepunkte: Die zweite Ableitung

$\displaystyle f^{\prime\prime}(x) = 2\sin x -12\cos^2 x \,\sin x=\sin x(6\sin^2x-5) $

ist Null für $ \sin x =0$ oder $ \sin x =\pm \sqrt{5/6}$, d.h.

$\displaystyle x=0 \quad\lor\quad x=\pm \pi \quad\lor\quad x=\pm a \quad\lor\quad x = \pm(\pi-a) $

mit $ a = \operatorname{arcsin}\sqrt{5/6}\approx {\tt 1.1503}$. Da die dritte Ableitung an diesen Stellen nicht verschwindet, hat $ f$ also Wendepunkte bei $ (0,0)$, $ (\pm \pi,0)$, $ (\pm a,\pm b)$ und $ (\pm(\pi-a),\pm b)$ mit

$\displaystyle b = f(a) = \sin a\,(2-(4/3)\sin^2 a) = \sqrt{5/6}\,(2-(4/3)(5/6)) \approx {\tt0.8114} \,, $

denn $ \sin a = \sin(\pi-a)$ und $ f(-a) = -f(a)$.

Asymptoten: Die Funktion ist periodisch und nicht konstant, hat also keine Asymptoten.

\includegraphics[width=10.4cm]{Kurvendiskussion_1}
Es wird eine Funktionsuntersuchung für die Funktion

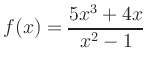
$\displaystyle f(x)=\frac{5x^3+4x}{x^2-1} $

durchgeführt.

Symmetrie: Der Zähler ist ungerade und der Nenner gerade. Die Funktion ist also ungerade, d.h. punktsymmetrisch zum Ursprung.

Periodizität: Die Funktion ist nicht periodisch.

Unstetigkeitsstellen und Polstellen: Der Nenner besitzt bei $ x=\pm 1$ einfache Nullstellen. Da der Zähler an diesen Punkten nicht Null ist, sind die Definitionslücken nicht hebbar, und $ -1$ und $ 1$ sind einfache Polstellen.

Nullstellen: Der Zähler verschwindet für $ x=0$.

Extrema: Die Ableitung

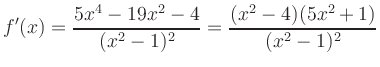
$\displaystyle f^\prime(x) = \frac{5x^4-19x^2-4}{(x^2-1)^2} = \frac{(x^2-4)(5x^2+1)}{(x^2-1)^2} $

verschwindet bei $ x = \pm 2$. Der Typ dieser kritischen Punkte kann aus dem qualitativen Verhalten von $ f$ gefolgert werden. Zunächst besitzt $ f$ wegen der einfachen Polstellen, an denen das Vorzeichen wechselt, keine globalen Extrema. Da $ f(x)\to-\infty$ für $ x\to -\infty$ und $ x\to -1$, muss das Intervall $ \left(-\infty,-1 \right)$ ein lokales Maximum enthalten. Analog enthält $ \left( 1, \infty \right)$ mindestens ein lokales Minimum. Zu den beiden einzigen Nullstellen der Ableitung erhält man also ein lokales Maximum bei $ (-2,-4/5)$ und ein lokales Minimum bei $ (2,4/5)$.

Wendepunkte: Die zweite Ableitung

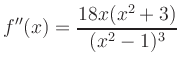
$\displaystyle f^{\prime\prime}(x) = \frac{18x(x^2+3)}{(x^2-1)^3} $

wechselt an der einzigen Nullstelle $ x=0$ das Vorzeichen; folglich ist $ (0,0)$ ein Wendepunkt.

Asymptoten: Mit Polynomdivision erhält man

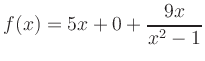
$\displaystyle f(x) = 5x + 0 + \frac{9x}{x^2-1} $

und somit $ p(x)=5x$ als Asymptote.

\includegraphics[width=10.4cm]{Kurvendiskussion_2}
Es wird eine Funktionsuntersuchung der Funktion

$\displaystyle f(x) = \vert x^2-1\vert$e$\displaystyle ^{-4x/3} $

durchgeführt.

(i) Qualitatives Verhalten: Wie die Exponentialfunktion besitzt auch $ f$ keine Symmetrien und ist nicht periodisch.

Unstetigkeitsstellen der Ableitung (Knicke) treten für $ x=\pm 1$ aufgrund des Knicks der Betragsfunktion bei dem Argument 0 auf.

Da $ \lim_{x\to\infty}x^r\exp(-sx) = 0$ für alle $ r,s>0$ ist $ p(x) = 0$ Asymptote für $ x\to\infty$. Für $ x\to-\infty$ existiert keine Asymptote, da $ \lim_{x\to-\infty}\vert f(x)/x\vert=\infty$.

(ii) Nullstellen: Wegen der Positivität der Exponentialfunktion werden die Nullstellen durch den ersten Faktor bestimmt und liegen bei $ x_{1,2}=\pm 1$. Da $ f\ge0$ sind die Nullstellen ebenfalls globale Minima. Ein globales Maximum existiert nicht, denn $ \lim_{x\to-\infty}f(x) = \infty$.

(iii) Extrema: Da $ f(-1) = f(1) = \lim_{x\to\infty}f(x)= 0$ enthalten die Intervalle $ (-1,1)$ und $ (1,\infty)$ jeweils mindestens ein lokales Maximum.

Ableiten von

$\displaystyle f(x) = \sigma (x^2-1)$e$\displaystyle ^{-4x/3},\quad x\ne\pm1\,, $

mit $ \sigma = -1$ für $ x\in(-1,1)$ und $ \sigma = 1$ für $ x\in(-\infty,-1)\cup(1,\infty)$ ergibt

$\displaystyle f^\prime(x) = \sigma \left[-4x^2/3+4/3+2x\right]$e$\displaystyle ^{-4x/3} \,. $

Durch Nullsetzen des quadratischen Polynoms in eckigen Klammern erhält man die kritischen Punkte $ x_3=-1/2$ und $ x_4=2$. An beiden Stellen hat $ f$ ein lokales Maximum wegen der Existenz von mindestens zwei solcher Extrema. Die entsprechenden Funktionswerte sind

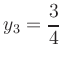$\displaystyle y_3 = \frac{3}{4}$e$\displaystyle ^{-2/3} \approx {\tt 1.4608}, \quad y_4 = 3$e$\displaystyle ^{-8/3} \approx {\tt0.2085} \,. $

(iv) Wendepunkte: Die Nullstellen von

$\displaystyle f^{\prime\prime}(x) = \sigma\left[16x^2/9-16x/3+2/9\right]$e$\displaystyle ^{-4x/3} $

bzw. von $ [\ldots]$ sind

$\displaystyle x_5 = 3/2-\sqrt{34}/4 \approx {\tt0.0423},\quad x_6 = 3/2+\sqrt{34}/4 \approx {\tt 2.9577} \,. $

In beiden Fällen handelt es sich um Wendepunkte, da $ f^{\prime\prime}$ dort das Vorzeichen wechselt. Die Funktionswerte sind

$\displaystyle y_5 \approx {\tt0.9435},\quad y_6 \approx {\tt0.1501} \,. $

\includegraphics[width=10.4cm]{Kurvendiskussion_3}
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009