Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Lineare Algebra und Geometrie - Vektoren

Skalarprodukt

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Das Skalarprodukt zweier Vektoren ist durch
$\displaystyle \vec{a}\cdot\vec{b}$ $\displaystyle =$ $\displaystyle \vert\vec{a}\vert\vert\vec{b}\vert\cos\sphericalangle(\vec{a},\vec{b})$  
  $\displaystyle =$ $\displaystyle a_1 b_1 + a_2 b_2 + a_3 b_3$  

definiert. Insbesondere ist

$\displaystyle \vec{a}\cdot\vec{a} = \vert\vec{a}\vert^2 $

und

$\displaystyle \vec{a}\cdot\vec{b} = 0 \quad \Leftrightarrow \quad \vec{a} \perp \vec{b}\, . $

Aus der Koordinatendarstellung des Skalarproduktes folgt

$\displaystyle \vec{a}\cdot\vec{b} = \vec{b}\cdot\vec{a} $

sowie

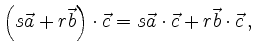
$\displaystyle \left(s\vec{a}+r\vec{b}\right)\cdot\vec{c} = s\vec{a}\cdot\vec{c}+r\vec{b}\cdot\vec{c}\, , $

d.h. es gelten die für Produkte üblichen Rechenregeln.

Das abgebildete Dreieck besitzt die Eckpunkte

$\displaystyle A=(6,0),\quad B=(4,4),\quad C = (0,0) $

und es ist

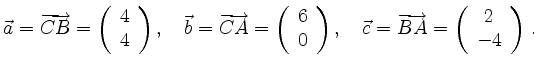
$\displaystyle \vec{a} = \overrightarrow{CB} = \left(\begin{array}{c} 4 \\ 4 \... ... \overrightarrow{BA} = \left(\begin{array}{c} 2 \\ -4 \end{array}\right)\, . $

\includegraphics[width=7.4cm]{bsp_skalar}

Der Winkel $ \gamma$ läßt sich mit Hilfe des Skalarproduktes berechnen:

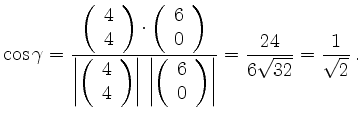
$\displaystyle \cos\gamma = \frac{ \left(\begin{array}{c} 4 \\ 4 \end{array}\r... ...array}\right)\right\vert } = \frac{24}{6\sqrt{32}} = \frac{1}{\sqrt{2}}\, . $

Man erhält $ \gamma = \pi/4$ , wie auch unmittelbar aus den Koordinaten ersichtlich ist.

Anhand des betrachteten Beispiels kann auch der Kosinussatz überprüft werden. Es gilt

$\displaystyle \vert\vec{c}\vert^2 - \vert\vec{a}\vert^2 - \vert\vec{b}\vert^2 = 20 - 32 - 36 = -48\, , $

was mit

$\displaystyle -2\vert\vec{a}\vert \vert\vec{b}\vert\cos\gamma = -2\,(4\sqrt{2})\,6 / \sqrt{2} $

übereinstimmt.

(Autoren: Höllig/Much)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009