Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Grundlagen - Aussagenlogik

Indirekter Beweis

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Um zu zeigen, dass aus Voraussetzungen $ V$ eine Behauptung $ B$ folgt ( $ V \Longrightarrow B$), kann man die Annahme, dass die Aussage $ B$ bei Gültigkeit der Voraussetzungen $ V$ falsch ist, zu einem Widerspruch führen:

$\displaystyle V\land(\lnot B)\,\Longrightarrow\,F \,, $

mit einer falschen Aussage $ F$, insbesondere $ F = \lnot V$ oder $ F=B$.

Speziell gilt

$\displaystyle B = (\lnot B \Longrightarrow F) \,=\,(\lnot B\Rightarrow B) \,, $

falls keine Voraussetzungen getroffen sind.
Die Implikation

$\displaystyle V \land (\lnot B)\,\Longrightarrow\,F $

ist äquivalent zu

$\displaystyle \lnot(V\land(\lnot B)) \lor F = (\lnot V) \lor B \lor F \,. $

Ist die Implikation wahr, das heißt wurde sie aus gültigen mathematischen Gesetzen gefolgert, so muss die Behauptung $ B$ wahr sein, denn $ \lnot V$ ist falsch und $ F$ ist entweder falsch oder gleich $ B$.

(Autoren: Höllig/Hörner)
Zur Illustration der indirekten Beweismethode wird gezeigt, dass $ \sqrt{2}$ irrational ist, d.h. nicht als Bruch darstellbar ist.

Man nimmt an, dass die Behauptung $ B$ falsch ist. Es gelte also

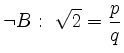$\displaystyle \lnot B:\ \sqrt{2} = \frac{p}{q}$   mit$\displaystyle \ p,q\in\mathbb{N},\quad \operatorname{ggT}(p,q)=1 \,. $

Dabei bezeichnet $ \operatorname{ggT}$ den größten gemeinsamen Teiler.

Aus der Annahme folgt durch Quadrieren und Multiplikation mit $ q^2$

$\displaystyle 2q^2 = p^2 \,, $

d.h. $ p^2$ und damit auch $ p$ ist eine gerade Zahl. Insbesondere existiert ein $ r\in\mathbb{N}$ mit $ p=2r$. Wegen

$\displaystyle q^2 = 2r^2 $

ist $ q$ ebenfalls gerade, und damit besitzen $ p$ und $ q$ den gemeinsamen Teiler $ 2$. Dies steht im Widerspruch zu dem Bestandteil der Annahme $ \lnot B$, dass $ \operatorname{ggT}(p,q)=1$, d.h.

$\displaystyle (\lnot B) \Longrightarrow B \,. $

Folglich muss die Behauptung $ B$ wahr sein.

(Autoren: Höllig/Knesch)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009