Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Analysis - Funktionen

Zinseszins

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Ein Startkapital $ x$ ergibt nach $ n$ -facher Aus- bzw. Einzahlung einer Rate $ r$ ($ r<0$ bzw. $ r>0$ ) bei einem Zinsfaktor $ (1+p)$ das Endkapital

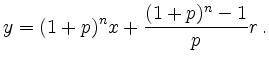
$\displaystyle y = (1+p)^nx + \frac{(1+p)^n - 1}{p} r\, . $

Dabei entspricht $ p=1$ einem Zinssatz von $ 100\%$ bei jährlichen Raten.

Der effektive Jahreszins $ p_j$ berechnet sich bei monatlicher Verzinsung mit einem Zinsatz $ p_m$ zu

$\displaystyle p_j=(1+p_m)^{12}-1 \geq 12p_m\,. $

Das Grundkapital wird bereits in der ersten Verzinsungsperiode berücksichtigt, die Ein- bzw. Auszahlungen erst ab der jeweils folgenden. Dies ergibt für

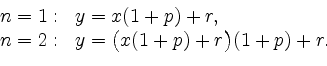
\begin{displaymath} \begin{array}{ll} n=1: & y = x(1+p) + r, \\ n=2: & y = \big(x(1+p) + r\big)(1+p) + r. \end{array}\end{displaymath}

Allgemein gilt

$\displaystyle y$ $\displaystyle =$ $\displaystyle \big(\cdots\big(x(1+p)+r\big)(1+p)+r\big)\cdots\big)$  
  $\displaystyle =$ $\displaystyle x(1+p)^n+\Big[1+(1+p)+(1+p)^2+\cdots+(1+p)^{n-1}\Big] r$  

Der Ausdruck in eckigen Klammern läßt sich mit der geometrischen Summenformel umwandeln und man erhält die angegebene Formel.
(Autoren: Höllig/Hörner)
Ein Darlehen von 100000 Euro soll bei jährlichen Raten und einem Zinssatz von 5 % nach 10 Jahren zurückgezahlt werden. Mit

$\displaystyle y = 0\,, \ n = 10\,, \ p = 0.05\,, \ x = 100000 $

erhält man als Rate
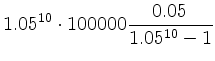$\displaystyle r$ $\displaystyle =$ $\displaystyle 1.05^{10} \cdot 100000 \frac{0.05}{1.05^{10}-1}$  
  $\displaystyle =$ $\displaystyle 12950.46$  

Bei einer monatlichen Verzinsung mit $ \frac{5}{12}\%$ ergibt sich mit

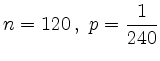
$\displaystyle n = 120\,, \ p = \frac{1}{240} $

entsprechend
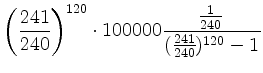$\displaystyle r$ $\displaystyle =$ $\displaystyle \left(\frac{241}{240}\right)^{120} \cdot 100000 \frac{\frac{1}{240}}{(\frac{241}{240})^{120}-1}$  
  $\displaystyle =$ $\displaystyle 1060.66$  

als monatliche Rate, im Jahr also 12727.86. Es entsteht jedoch ein Verlust durch eine mögliche Verzinsung der zu früh gezahlten Beträge. Bei $ \frac{4}{12}$% wäre dieser gleich

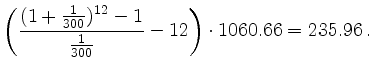
$\displaystyle \left(\frac{(1+\frac{1}{300})^{12}-1}{\frac{1}{300}} -12 \right) \cdot 1060.66 = 235.96\,. $

(Autoren: Höllig/Kreitz)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009