- a)
- Divergiert die Reihe
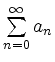 , so divergiert auch
die Folge
, so divergiert auch
die Folge 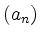 .
.
keine Angabe , wahr , falsch
- b)
- Ist die Funktion
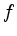 stetig auf
stetig auf
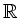 , so ist
sie auf jedem abgeschlossenen Intervall
, so ist
sie auf jedem abgeschlossenen Intervall
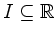 beschränkt.
beschränkt.
keine Angabe , wahr , falsch
- c)
- Es gibt unstetige Funktionen, die Lipschitz-stetig sind.
keine Angabe , wahr , falsch
- d)
- Die Funktionenfolge
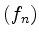 mit
mit
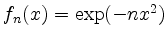 konvergiert
gleichmäßig auf
konvergiert
gleichmäßig auf
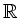 .
.
keine Angabe , wahr , falsch
- e)
- Konvergiert die Funktionenfolge
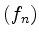 gleichmäßig auf
gleichmäßig auf
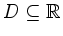 ,
dann konvergiert auch die Funktionenfolge
,
dann konvergiert auch die Funktionenfolge 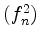 gleichmäßig auf
gleichmäßig auf 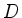 .
.
keine Angabe , wahr , falsch
Untersuchen Sie die folgenden Reihen auf Konvergenz.
Betrachtet werden Bakterien, die auf einem nährstoffreichen
Kulturmedium die Generationszeit 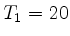 Minuten und auf einem nährstoffarmen
Kulturmedium die Generationszeit
Minuten und auf einem nährstoffarmen
Kulturmedium die Generationszeit 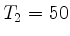 Minuten besitzen. Die Anfanspopulation
auf dem nährstoffarmen Kulurmedium sei zehnmal größer als die
Anfangspopulation auf dem nährstoffreichen Medium. Nach wie viel Minuten sind
die beiden Populationen gleich groß?
Minuten besitzen. Die Anfanspopulation
auf dem nährstoffarmen Kulurmedium sei zehnmal größer als die
Anfangspopulation auf dem nährstoffreichen Medium. Nach wie viel Minuten sind
die beiden Populationen gleich groß?

