Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Aufgabensammlung:

Aufgabe 100: Konvergenz von Reihen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

a)
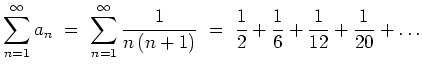
Gegeben sei die Reihe $ {\displaystyle{\sum_{n=1}^\infty a_n \ = \ \sum_{n=1}^\infty \frac{1}{n\,(n+1)} \ = \ \frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\ldots}}$

Schreiben Sie das allgemeine Reihenglied $ a_n$ als Differenz zweier Brüche. Konvergiert die Reihe, und wenn ja, welchen Grenzwert besitzt sie?

b)
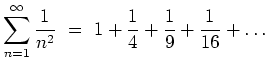Untersuchen Sie die Reihe $ {\displaystyle{\sum_{n=1}^\infty \frac{1}{n^2} \ = \ 1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\ldots}}$ auf Konvergenz.

Hinweis: Verwenden Sie a).

(Aus: HM I Kimmerle/Roggenkamp WS 97/98)

siehe auch:

[Lösungen]
  automatisch erstellt am 2.  9. 2005