Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung:

Aufgabe 1493: Totale Ableitung und lokale Extrema

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Sei $ f:{\mathbb{R}}^2\to{\mathbb{R}}$ und $ \boldsymbol{x}_0\in{\mathbb{R}}^2$
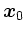  1. Geben Sie eine notwendige und hinreichende Bedingung für die Existenz der totalen Ableitung von $ f$ in $ \boldsymbol{x}_0$ an. (Nicht die Definition!)

  2. Geben Sie den Zusammenhang zwischen der Richtungsableitung im Punkte 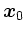$ \boldsymbol{x}_0$ in Richtung $ \boldsymbol{a}$ und dem Gradienten von $ f$ an.

  3. Sei $ f$ zusätzlich 2 mal stetig differenzierbar.
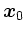
    1. Formulieren Sie die notwendige Bedingung für ein lokales Extrema von $ f$ in $ \boldsymbol{x}_0$

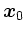    2. Formulieren Sie eine hinreichende Bedingung für ein lokales Minimum von $ f$ in $ \boldsymbol{x}_0$, die wesentlich auf die 2. Ableitungen zurückgreift.

(Aus: Mathematik II für Informatik und Softwaretechnik SS06, Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)

Lösung:

[Verweise]
  automatisch erstellt am 13. 10. 2006