Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung:

Aufgabe 311: Volumenberechnung eines Körpers, Vertauschung der Integrationsreihenfolge

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Deuten Sie das Integral

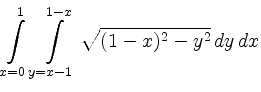
$\displaystyle \int \limits_{x=0}^1 \int \limits_{y=x-1}^{1-x}\sqrt{(1-x)^2-y^2}\, dy\,dx $

geometrisch als Volumen eines Körpers. Berechnen Sie den Wert des Integrals, indem Sie die Reihenfolge der Integrationen geschickt wählen, und verifizieren Sie das Ergebnis durch Anwendung der bekannten Formel aus der Formelsammlung.
(Aus: HM III mach, bau, umw WS 2002/03)

Lösung:

[Verweise]
  automatisch erstellt am 22.  7. 2008