Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung:

Aufgabe 754: Approximation von Ableitungen mit diskreter Fourier-Transformation und Näherungslösung einer Differentialgleichung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Sind die Funktionswerte $ (u_0, u_1, \dots, u_{n-1})^{\rm {t}}$ einer $ 2\pi$-periodischen Funktion $ u$ an den Stellen $ 0, h, \dots, (n-1)h$, $ h=2\pi / n$, bekannt, so lassen sich die Funktionswerte der Ableitung näherungsweise durch

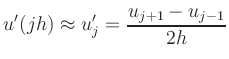
$\displaystyle u^\prime(jh) \approx u_j'=\frac{u_{j+1}-u_{j-1}}{2h} $

berechnen.

Wie lässt sich die diskrete Fourier-Transformation von $ (u_0', u_1', \dots, u_{n-1}'\,)^{\rm {t}}$ aus der von $ (u_0, u_1, \dots, u_{n-1})^{\rm {t}}$ berechnen? Welche Approximation ergibt sich für die zweite Ableitung.

Berechnen Sie mit Hilfe die Näherungen eine numerische Lösung für die Differentialgleichung

$\displaystyle -u^{\prime\prime} + u = f(x),\quad 0 \leq x < 2 \pi \,. $

(Autor: Klaus Höllig)

siehe auch:

  automatisch erstellt am 26.  3. 2018