Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

p-integrierbare Funktionen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Für ein Gebiet $ D\subseteq\mathbb{R}^n$ bezeichnet $ L^p(D)$, $ 1\le p<\infty$, den Banach-Raum der Funktionen, die bezüglich der Norm

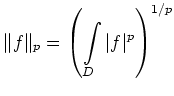
$\displaystyle \Vert f\Vert _p =\left(\int\limits_D\vert f\vert^p\right)^{1/p} $

durch stetige Funktionen mit kompaktem Träger approximierbar sind, d. h. $ L^p(D)$ ist der Abschluß von $ C_0(D)$ bezüglich $ \Vert\cdot\Vert _p$.

Funktionen $ f\in L^p(D)$ sind punktweise nur bis auf Mengen vom Maß Null definiert. Man schreibt

$\displaystyle f=g$    f. ü. (fast überall) bzw. a. e. (almost everywhere)

für Funktionen, die sich nur auf einer Nullmenge unterscheiden und identifiziert solche Funktionen. Genauer betrachet man die Äquivalenzklasse, für die $ f$ oder $ g$ ein Repräsentant ist.

Mit Hilfe des Lebesgue-Integrals kann $ L^p(D)$ allgemein für beliebige Lebesgue-meßbare Mengen definiert werden. Zur Approximation werden dann, analog zum Riemann-Integral, Treppenfunktionen verwendet, die auf Lebesgue-meßbaren Teilmengen von $ D$ konstant sind.

siehe auch:

  automatisch erstellt am 19.  8. 2013