Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Stetiges lineares Funktional

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Ein stetiges lineares Funktinal $ \Lambda$ auf einem reellen (komplexen) topologischen Vektorraum $ V$ ist eine stetige lineare Abbildung von $ V$ nach $ \mathbb{R}$ ( $ \mathbb{C}$).

In einem normierten Vektorraum ist Stetigkeit von $ \Lambda$ äquivalent zu der Beschränktheit des Bildes der Einheitskugel um Null. Man definiert in diesem Fall

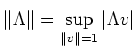
$\displaystyle \Vert\Lambda\Vert =\sup_{\Vert v\Vert=1}\vert\Lambda v\vert $

als die Norm des linearen Funktionals.

Aufgrund der Homogenität der Norm, sind ebenfalls die äquivalenten Definitionen

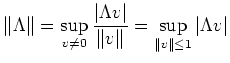
$\displaystyle \Vert\Lambda\Vert=\sup_{v\ne 0}\frac{\vert\Lambda v\vert}{\Vert v\Vert} =\sup_{\Vert v\Vert\le 1}\vert\Lambda v\vert $

möglich.

siehe auch:

[Erläuterungen] [Beispiele]
  automatisch erstellt am 19.  8. 2013