Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Faltung von temperierten Distributionen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Für eine temperierte Distribution $ \Lambda \in \mathcal{S}'$ und eine schnell abfallende Testfunktion $ \varphi \in \mathcal{S}$ ist durch

$\displaystyle \left(\Lambda \star \varphi\right)(x) = \Lambda \varphi(x-\cdot) $

eine Faltung definiert.

Die Funktion $ \Lambda \star \varphi$ ist unendlich oft differenzierbar und schwach wachsend, kann also mit einer temperierten Distribution identifiziert werden.

Ist $ \Lambda=\Lambda_\psi$ mit $ \psi \in \mathcal{D}$, so ist

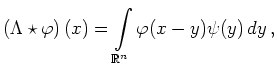
$\displaystyle \left( \Lambda \star \varphi\right) (x) = \int\limits_{\mathbb{R}^n} \varphi(x-y)\psi(y)\,dy\,, $

die Faltung mit Distributionen verallgemeinert also die übliche Definition für Funktionen.

siehe auch:

  automatisch erstellt am 19.  8. 2013