Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Algorithmus für das cg-Verfahren

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Für die Gradienten $ g_k$ und Suchrichtungen $ u_k$ des cg-Verfahrens gilt die Beziehung

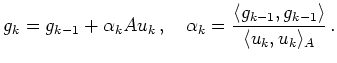
$\displaystyle g_k = g_{k-1}+\alpha_k A u_k\,,\quad \alpha_{k} = \frac{\langle g_{k-1},g_{k-1}\rangle}{\langle u_{k},u_{k}\rangle_A}\,. $

Es ist also möglich, bei einer Implementierung des cg-Verfahrens mit einer Matrix-Vektor-Multiplikation pro Iterationsschritt auszukommen.

Speichert man zusätzlich noch die mehrfach verwendeten Skalarprodukte, kann das cg-Verfahren durch folgende MATLAB-Sequenz implementiert werden: 

x=x0;
g=A*x-b
u=-g;
gamma=g'*g;
while gamma > tol
  Au=A*u;
  alpha=gamma/(u'*Au);
  x=x+alpha*u
  g=g+alpha*Au
  beta=gamma;
  gamma=g'*g;
  beta=gamma/beta;
  u=beta*u-g
end
[Verweise]
  automatisch erstellt am 19.  8. 2013