Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Trapez-Regel für eine Differentialgleichung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Integriert man die Lösung $ (u_1(t),\ldots,u_d(t))^t$ eines Differentialgleichungssystems

$\displaystyle u^\prime = f(t,u) \,, $

so folgt

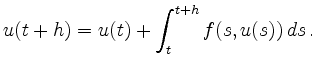
$\displaystyle u(t+h) = u(t) + \int_t^{t+h}f(s,u(s))\,ds \,. $

Das Integral kann durch die Trapezregel angenähert werden. Ein Schritt $ u(t)\approx v \to w \approx u(t+h)$ des resultierenden Verfahrens hat dann die Form

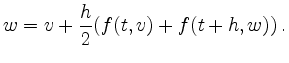
$\displaystyle w = v + \frac{h}{2}(f(t,v)+f(t+h,w)) \,. $

Die Trapezregel ist ein implizites Einschrittverfahren der Ordnung $ 2$.

Zur Durchführung eines Verfahrensschritts $ v\to w$ muss im allgemeinen ein nichtlineares Gleichungssystem gelöst werden. Näherungsweise kann dies durch einige wenige Schritte einer Fixpunktiteration

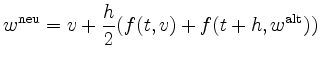
$\displaystyle w^{\mathrm{neu}} = v + \frac{h}{2}(f(t,v)+f(t+h,w^{\mathrm{alt}})) $

mit Startwert $ w=v$ geschehen.

Für ein lineares Differentialgleichungssystem

$\displaystyle u^\prime = A(t)u + b(t) $

ist die Trapezregel einfacher realisierbar. Ein Schritt erfordert lediglich die Lösung des linearen Gleichungssystems

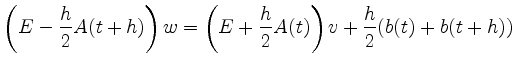
$\displaystyle \left(E-\frac{h}{2} A(t+h)\right) w = \left(E+\frac{h}{2} A(t)\right) v + \frac{h}{2}(b(t) + b(t+h)) $

mit $ E$ der $ d\times d$-Einheitsmatrix.

siehe auch:

[Erläuterungen] [Beispiele]
  automatisch erstellt am 19.  8. 2013