Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Runge-Kutta-Verfahren

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Bei einem Zeitschritt

$\displaystyle v \approx u(t) \rightarrow u(t+h) \approx w $

eines $ n$ -stufigen Runge-Kutta-Verfahrens zur Approximation des Differentielgleichungssystems

$\displaystyle u^\prime =f(t,u) $

werden zunächst die $ n$ Hilfsgrößen

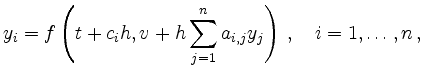
$\displaystyle y_i = f \left( t+c_i h, v+h \sum\limits_{j=1}^n a_{i,j} y_j \right) \,, \quad i=1,\ldots,n\,, $

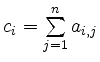mit $ c_i=\sum\limits_{j=1}^n a_{i,j}$ berechnet und dann die gewichtete Summe

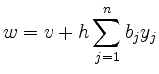
$\displaystyle w=v+h \sum\limits_{j=1}^n b_j y_j $

gebildet.

Die Approximationsordnung hängt von der Wahl der Verfahrensparameter

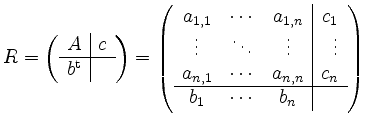
$\displaystyle R = \left( \begin{array}{r\vert r} A & c \\ \hline b^{\operatorna... ... \cdots & a_{n,n} & c_n \\ \hline b_{1} & \cdots & b_{n} & \end{array} \right) $

ab.

Ist

$\displaystyle a_{i,j} =0 \,, \quad j \geq i \,, $

so lassen sich die Hilfsgrößen $ y_i$ sukzessive berechnen, und das Verfahren ist explizit. Andernfalls müssen die Hilfsgrößen simultan durch Lösen eines nichtlinearen Gleichungssystems bestimmt werden. Solche impliziten Runge-Kutta-Verfahren sind deshalb in erster Linie für lineare Differentialgleichungen geeignet.

siehe auch:

  automatisch erstellt am 19.  8. 2013