Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Algorithmus für Runge-Kutta-Verfahren

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Die Parameter für ein $ n$-stufiges Runge-Kutta-Verfahren können in einer $ (n+1)\times(n+1)$-Matrix $ R$ zusammengefaßt werden

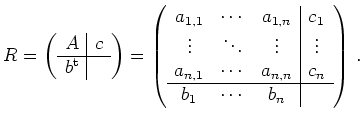
$\displaystyle R = \left(\begin{array}{c\vert c} A & c \\ \hline b^ \mathrm{t} &... ... & \cdots & a_{n,n} & c_n \\ \hline b_1 & \cdots & b_n & \end{array}\right)\,. $

Speichert man auch die Hilfsgrößen $ w_j$ in einer Matrix $ W=\left(w_1,w_2,\ldots,w_n\right)$, so läßt sich das Runge-Kutta-Verfahren einfach implementieren. Folgende MATLAB-Sequenz führt einen Schritt eines $ n$-stufigen expliziten Runge-Kutta-Verfahrens durch. 

W=zeros(length(v),n);
for j=1:n
   W(:,j)=feval(f,v+h*W*R(j,1:n)',t+h*R(j,n+1));
end
v=v+h*W*R(n+1,1:n)';

Für ein implizites Verfahren, ist im Allgemeinen ein nichtlineares Gleichungssystem zu lösen. Dies kann z.B. mit dem Newton-Verfahren erfolgen. Die Funktion, deren Nullstelle dabei zu suchen ist, wird durch folgende MATLAB-Seqeunz beschrieben. 

for j=1:n
   NF(:,j)=feval(f,v+h*W*R(j,1:n)',t+h*R(j,n+1))-W(:,j);
end

siehe auch:

  automatisch erstellt am 19.  8. 2013