
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Folgenkonvergenz |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Begriff.
Eine Folge komplexer Zahlen
![]() , wobei
, wobei
![]() , konvergiert gegen
, konvergiert gegen
![]() , falls
es zu jedem reellen
, falls
es zu jedem reellen
![]() eine Schranke
eine Schranke
![]() gibt mit
gibt mit
Ist
![]() , oder äquivalent, ist
, oder äquivalent, ist
![]() , so heißt
, so heißt
![]() eine
Nullfolge.
eine
Nullfolge.
Nicht konvergente Folgen heißen divergent.
Bestimmt divergente Folgen.
Es sei
![]() eine reellwertige Folge.
Gibt es für alle
eine reellwertige Folge.
Gibt es für alle
![]() eine Schranke
eine Schranke
![]() mit
mit
![]() für alle
für alle
![]() , so heißt
, so heißt
![]() bestimmt divergent gegen
bestimmt divergent gegen
![]() , und wir schreiben
auch
, und wir schreiben
auch
![]() oder
oder
![]() (ohne daß dies eine Konvergenzbehauptung einschließt).
(ohne daß dies eine Konvergenzbehauptung einschließt).
Gibt es für alle
![]() eine Schranke
eine Schranke
![]() mit
mit
![]() für alle
für alle
![]() , so heißt
, so heißt
![]() bestimmt divergent gegen
bestimmt divergent gegen
![]() , und wir schreiben
auch
, und wir schreiben
auch
![]() oder
oder
![]() .
.
Regeln.
Seien
![]() ,
,
![]() konvergente Folgen, seien
konvergente Folgen, seien
![]() . Es gelten die folgenden Grenzwertregeln.
. Es gelten die folgenden Grenzwertregeln.
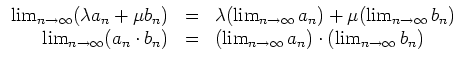
Ist
![]() eine reellwertige bestimmt divergente Folge, so ist
eine reellwertige bestimmt divergente Folge, so ist
![]() eine Nullfolge.
eine Nullfolge.
Folgen definiert durch rationale Funktionen.
Ist
![]() ein reelles Polynom von Grad
ein reelles Polynom von Grad
![]() , so ist die Folge
, so ist die Folge
![]() bestimmt divergent, und zwar gegen
bestimmt divergent, und zwar gegen
![]() bzw. gegen
bzw. gegen
![]() , falls der führende Koeffizient von
, falls der führende Koeffizient von
![]() positiv bzw. negativ ist.
positiv bzw. negativ ist.
Speziell sind zum Beispiel die Folgen
![]() ,
,
![]() , etc. Nullfolgen.
, etc. Nullfolgen.
Sind
![]() und
und
![]() komplexe Polynome, sei
komplexe Polynome, sei
![]() , und hat
man die Folge
, und hat
man die Folge
![]() auf Konvergenz zu untersuchen, so kürze man diesen Bruch mit
auf Konvergenz zu untersuchen, so kürze man diesen Bruch mit
![]() und wende dann die
Grenzwertregeln an.
und wende dann die
Grenzwertregeln an.
Einfache Kriterien.
Jede konvergente Folge ist beschränkt. Ist
![]() beschränkt und
beschränkt und
![]() eine Nullfolge, so ist auch
eine Nullfolge, so ist auch
![]() eine Nullfolge.
eine Nullfolge.
Seien nun
![]() ,
,
![]() und
und
![]() reellwertige Folgen mit
reellwertige Folgen mit
![]() für alle
für alle
![]() , und
mit
, und
mit
![]() . Dann ist nach dem Vergleichskriterium
. Dann ist nach dem Vergleichskriterium
Sei schließlich
![]() eine monotone beschränkte Folge. Dann ist
eine monotone beschränkte Folge. Dann ist
![]() nach dem
Monotoniekriterium konvergent. Ist
nach dem
Monotoniekriterium konvergent. Ist
![]() monoton wachsend, so ist
monoton wachsend, so ist
![]() ; ist
; ist
![]() monoton fallend, so ist
monoton fallend, so ist
![]() .
.
Limes superior, Limes inferior.
Sei
![]() eine Folge reeller Zahlen. Eine Teilfolge von
eine Folge reeller Zahlen. Eine Teilfolge von
![]() ist eine Folge der
Form
ist eine Folge der
Form
![]() , wobei
, wobei
![]() eine streng monoton wachsende Folge ist.
eine streng monoton wachsende Folge ist.
Ein Punkt
![]() heißt Häufungspunkt von
heißt Häufungspunkt von
![]() , wenn es eine Teilfolge
, wenn es eine Teilfolge
![]() gibt mit
gibt mit
![]() .
.
Nach Bolzano-Weierstraß hat jede reelle Folge wenigstens einen Häufungspunkt in
![]() .
.
Eine Folge ist konvergent, wenn sie genau einen Häufungspunkt besitzt, und dieser in
![]() liegt.
liegt.
Sei
![]() die Menge der Häufungspunkte von
die Menge der Häufungspunkte von
![]() . Es ist der Limes inferior von
. Es ist der Limes inferior von
![]() gegeben
durch
gegeben
durch
Ist die Folge
![]() nach oben unbeschränkt, so ist
nach oben unbeschränkt, so ist
![]() ; ist sie nach unten
unbeschränkt, so ist
; ist sie nach unten
unbeschränkt, so ist
![]() .
.
Stimmen Limes inferior und Limes superior überein, so ist
![]() .
.
Beispiele:
| automatisch erstellt am 25. 1. 2006 |