Mathematik-Online-Lexikon: Exponentialfunktion

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Lexikon:
	Exponentialfunktion

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Übersicht

Exponentialfunktion.

Die Exponentialfunktion ist eine komplexe Funktion, definiert durch

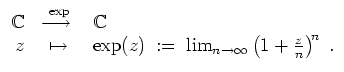
$\mbox{$\displaystyle \begin{array}{rcl} \mathbb{C}& \unitlength.1mm\begin{pic... ...z) \; :=\; \lim_{n\to\infty}\left(1+\frac{z}{n}\right)^{\! n}\; . \end{array}$}$

Als Potenzreihe ergibt sich

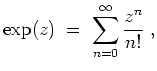
$\mbox{$\displaystyle \exp(z) \; =\; \sum_{n = 0}^\infty \frac{z^n}{n!}\; , $}$

worauf wir später nochmals eingehen werden.

Die Zahl $\mbox{$e := \exp(1) = \lim(1+\frac{1}{n})^n$}$ heißt Eulersche Zahl. Es ist $\mbox{$e = 2.71828182845\ldots$}$ .

Ist $\mbox{$x\in\mathbb{R}$}$ , so ist auch $\mbox{$\exp(x)\in\mathbb{R}$}$ .

Es gelten die folgenden Rechenregeln für $\mbox{$z,w\in\mathbb{C}$}$ und $\mbox{$x,y\in\mathbb{R}$}$ .

$\mbox{$\exp(x) > 0$}$ .
$\mbox{$x < y$}$ $\mbox{$\Longrightarrow $}$ $\mbox{$\exp(x) < \exp(y)\;,\;\;$}$ d.h. die reelle Exponentialfunktion ist streng monoton wachsend.
$\mbox{$\exp(x) \geq x + 1$}$ .
$\mbox{$\exp(0) = 1$}$ .
$\mbox{$\exp(z+w) = \exp(z)\cdot\exp(w)$}$ .
$\mbox{$\exp(-z) = \exp(z)^{-1}$}$ .

Insbesondere ist $\mbox{$\exp(x) = e^x$}$ für $\mbox{$x\in\mathbb{Q}$}$ , z.B. $\mbox{$\exp(-2/3) = \sqrt[3]{e^{-2}}$}$ .

Die reelle Exponentialfunktion ist streng monoton wachsend und nimmt alle positiven Werte an.

Der Graph der reellen Exponentialfunktion hat folgende Gestalt.

$\includegraphics[width=10cm]{exp.eps}$

Logarithmus.

Wegen der strengen Monotonie der reellen Exponentialfunktion besitzt sie eine Umkehrfunktion

$\mbox{$\displaystyle \log\; : \mathbb{R}_{>0}\longrightarrow \mathbb{R}\;,\;\; x\mapsto \log x\ , $}$

den Logarithmus.

Für $\mbox{$x,y\in\mathbb{R}_{>0}$}$ gelten die folgenden Rechenregeln.

$\mbox{$x < y$}$ $\mbox{$\Longrightarrow $}$ $\mbox{$\log x < \log y\;,\;\;\;$}$ d.h. der Logarithmus ist streng monoton wachsend.
$\mbox{$\log x \leq x - 1$}$ .
$\mbox{$\log 1 = 0$}$ .
$\mbox{$\log(xy)\; = \; \log x + \log y$}$ .
$\mbox{$\log(1/x)\; = \; -\log x$}$ .

Ferner gelten folgende Zusammenhänge zwischen der Exponentialfunktion und dem Logarithmus.

$\mbox{$\exp(\log x)=x$}$ für $\mbox{$x\in\mathbb{R}_{>0}$}$ .
$\mbox{$\log(\exp(x))=x$}$ für $\mbox{$x\in\mathbb{R}$}$ .

Der Logarithmus ist streng monoton wachsend und nimmt alle reellen Werte an.

Der Graph des Logarithmus hat folgende Gestalt.

$\includegraphics[width=10cm]{log.eps}$

Allgemeine Potenzfunktion.

Für $\mbox{$a>0$}$ und $\mbox{$z\in\mathbb{C}$}$ definiert man die allgemeine Potenzfunktion durch

$\mbox{$\displaystyle a^z\; :=\; \exp(z\log a)\ . $}$

Diese Definition stimmt im Fall $\mbox{$z\in\mathbb{Q}$}$ mit der üblichen Bedeutung überein. Z.B. ist $\mbox{$2^{3/5} = \exp(\frac{3}{5}\log 2) = \sqrt[5]{\exp(3\log 2)} = \sqrt[5]{\exp(\log(2^3))} = \sqrt[5]{2^3}$}$ .

Für $\mbox{$a,b>0$}$ , $\mbox{$x\in\mathbb{R}$}$ und $\mbox{$z,w\in\mathbb{C}$}$ gelten die folgenden Rechenregeln.

$\mbox{$a^0=1$}$ .
$\mbox{$a^1=a$}$ .
$\mbox{$(ab)^z=a^z\cdot b^z$}$ .
$\mbox{$a^{z+w}=a^z\cdot a^w$}$ .
$\mbox{$(a^x)^z=a^{xz}$}$ .
$\mbox{$\log(a^x) = \log(\exp(x\log a)) = x\log a$}$ .

(Autoren: Künzer/Martin/Nebe)

[Beispiele] [Verweise]

automatisch erstellt am 25. 1. 2006