Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Potenzreihen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Begriff.

Für eine Folge $ \mbox{$(a_n)_{n\geq 0}$}$ komplexer Zahlen sei

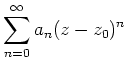
$ \mbox{$\displaystyle \sum_{n = 0}^\infty a_n (z-z_0)^n $}$
eine Potenzreihe in $ \mbox{$z$}$ um den Entwicklungspunkt $ \mbox{$z_0\in\mathbb{C}$}$. Ihr Konvergenzradius ist gegeben durch die Formel von Cauchy-Hadamard
$ \mbox{$\displaystyle R \; = \; 1\left/\left(\overline {\lim}_{n\to\infty}\sqrt[n]{\vert a_n\vert}\right)\right.\; . $}$
Hierbei ist $ \mbox{$1/0 = +\infty$}$ und $ \mbox{$1/\infty = 0$}$ zu setzen.

Die Potenzreihe

Falls 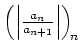$ \mbox{$\left(\left\vert\frac{a_n}{a_{n+1}}\right\vert\right)_{\! n}$}$ konvergiert oder bestimmt gegen $ \mbox{$+\infty$}$ divergiert, so ist

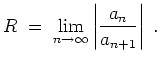
$ \mbox{$\displaystyle R \; =\;\lim_{n\to\infty} \left\vert\frac{a_n}{a_{n+1}}\right\vert\; . $}$

Sei $ \mbox{$B_R(z_0) \subseteq D \subseteq \overline {B_R(z_0)}$}$ der Definitionsbereich der Potenzreihe $ \mbox{$\sum_{n = 0}^\infty a_n (z-z_0)^n$}$, d.h. sei $ \mbox{$D$}$ die Menge der $ \mbox{$z\in\mathbb{C}$}$, in denen die Potenzreihe konvergiert. Dann ist

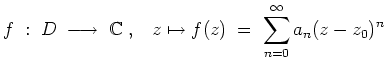
$ \mbox{$\displaystyle f\; :\; D\;\longrightarrow \; \mathbb{C}\; , \;\;\; z\mapsto f(z) \; =\; \sum_{n = 0}^\infty a_n (z-z_0)^n $}$
stetig auf $ \mbox{$D$}$.

In der Natur kommen Potenzreihen häufig als das Ergebnis von Taylorentwicklungen vor, wie wir später noch sehen werden.

Cauchyprodukt.

Das Produkt zweier Potenzreihen um $ \mbox{$z_0$}$ ist gegeben durch das Cauchyprodukt

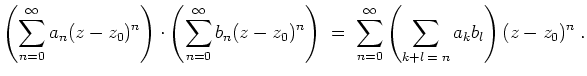
$ \mbox{$\displaystyle \left(\sum_{n = 0}^\infty a_n (z-z_0)^n\right)\cdot\left... ...; \sum_{n = 0}^\infty \left(\sum_{k+l\; =\; n} a_k b_l \right) (z-z_0)^n\; . $}$
Sein Konvergenzradius ist größer oder gleich dem Minimum der Konvergenzradien der Faktoren.

Elementare Funktionen.

Wir geben die Potenzreihendarstellungen der geläufigsten elementaren Funktionen samt Konvergenzradien. Sei hierbei $ \mbox{$\alpha\in\mathbb{C}\backslash \mathbb{N}$}$.

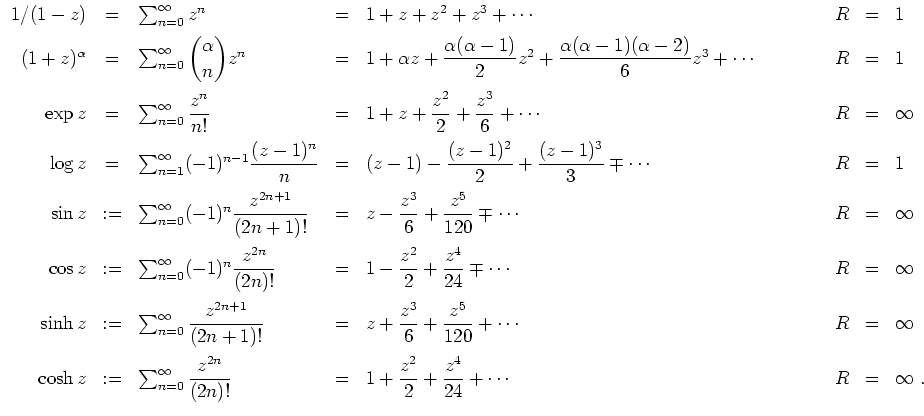
$ \mbox{$\displaystyle \begin{array}{rclclcrcl} 1/(1-z) & = & \displaystly\sum_... ...ac{z^4}{24}} + \cdots & \hspace*{1cm} & R & = & \infty\; . \\ \end{array}$}$

Für den Sinus $ \mbox{$\sin z$}$ und den Cosinus $ \mbox{$\cos z$}$ gilt folglich die Eulersche Identität

$ \mbox{$\displaystyle \exp(\mathrm{i}z) \; = \; \cos z + \mathrm{i}\sin z \; . $}$
Umgekehrt gilt
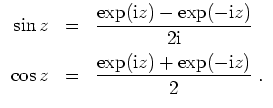
$ \mbox{$\displaystyle \begin{array}{rcl} \sin z & = & {\displaystyle\frac{\exp... ...aystyle\frac{\exp(\mathrm{i}z) + \exp(-\mathrm{i}z)}{2}}\; . \\ \end{array}$}$
Man definiert den Tangens durch
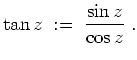
$ \mbox{$\displaystyle \tan z \; :=\; \frac{\sin z}{\cos z} \; . $}$

Analog gilt für den Sinus hyperbolicus $ \mbox{$\sinh(z)$}$ und den Cosinus hyperbolicus $ \mbox{$\cosh(z)$}$

$ \mbox{$\displaystyle \exp z \; = \; \cosh z + \sinh z \; . $}$
Umgekehrt gilt
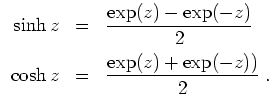
$ \mbox{$\displaystyle \begin{array}{rcl} \sinh z & = & {\displaystyle\frac{\ex... ...osh z & = & {\displaystyle\frac{\exp(z) + \exp(-z))}{2}}\; . \\ \end{array}$}$

Den Cosinus verwendet der Mathematiker zur Einführung der Kreiszahl $ \mbox{$\pi$}$, indem er $ \mbox{$\pi/2$}$ definiert als die kleinste positive Nullstelle von $ \mbox{$\cos x$}$ für $ \mbox{$x\in\mathbb{R}$}$.

Es gelten folgende Regeln.

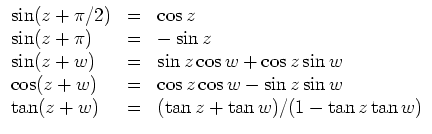
$ \mbox{$\displaystyle \begin{array}{lcl} \sin(z + \pi/2) & = & \cos z \\ \si... ... \\ \tan(z + w) & = & (\tan z + \tan w)/(1 - \tan z\tan w) \\ \end{array}$}$

Einige Werte von Sinus und Cosinus.

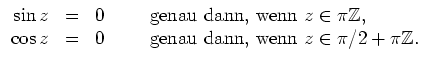
$ \mbox{$\displaystyle \begin{array}{rcl} \sin z & = & 0 \hspace*{1cm} \mbox{ge... ...ox{genau dann, wenn {$\mbox{$z\in\pi/2 + \pi\mathbb{Z}$}$}.} \\ \end{array}$}$
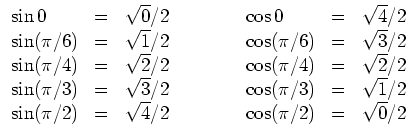
$ \mbox{$\displaystyle \begin{array}{lclclcl} \sin 0 & = & \sqrt{0}/2 & \hspace... ...sin(\pi/2) & = & \sqrt{4}/2 & & \cos(\pi/2) & = & \sqrt{0}/2 \\ \end{array}$}$
Geometrisch gesprochen verwenden wir für den Sinus das Bogenmaß. Ist ein Winkel $ \mbox{$\varphi \in [0,360]$}$ in Grad gegeben, so bekommt man das zugehörige Bogenmaß $ \mbox{$\varphi \cdot\pi/180$}$.
(Autoren: Künzer/Martin/Nebe)

siehe auch:

[Beispiele]
  automatisch erstellt am 25.  1. 2006