Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Differenzierbarkeit

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Offene Mengen.

Eine Teilmenge $ \mbox{$D\subseteq \mathbb{R}$}$ heißt offen, falls zu jedem $ \mbox{$x\in D$}$ ein $ \mbox{$\varepsilon >0$}$ so existiert, daß $ \mbox{$B_\varepsilon (x)\cap\mathbb{R}=(x-\varepsilon ,x+\varepsilon )\subseteq D$}$.

Zum Beispiel sind alle Intervalle der Form $ \mbox{$(a,b)$}$ mit $ \mbox{$a,b\in\hat{\mathbb{R}}$}$ und $ \mbox{$a<b$}$ offen. Beliebige Vereinigungen offener Mengen sind wieder offen.

Begriff.

Sei $ \mbox{$D\subseteq \mathbb{R}$}$ eine offene Teilmenge. Die Funktion

$ \mbox{$\displaystyle f \; : \; D\; \longrightarrow \; \mathbb{C}\; . $}$
heißt differenzierbar in $ \mbox{$x_0\in D$}$, falls der Grenzwert
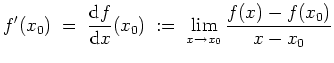
$ \mbox{$\displaystyle f'(x_0) \; =\; \frac{{\mbox{d}}f}{{\mbox{d}}x}(x_0) \;:=\; \lim_{x\to x_0} \frac{f(x) - f(x_0)}{x - x_0} $}$
existiert, genannt die Ableitung oder der Differentialquotient von $ \mbox{$f$}$ in $ \mbox{$x_0$}$.

Alternativ, $ \mbox{$f$}$ besitzt in $ \mbox{$x_0$}$ die Ableitung $ \mbox{$f'(x_0)$}$ genau dann, wenn eine Funktion $ \mbox{$r:D\longrightarrow \mathbb{C}$}$ existiert mit

$ \mbox{$\displaystyle f(x) \; =\; f(x_0) + f'(x_0)(x - x_0) + r(x)(x - x_0)\; , $}$
welche in $ \mbox{$x_0$}$ stetig ist mit $ \mbox{$r(x_0) = 0$}$. In diesem Sinne ist $ \mbox{$f(x_0) + f'(x_0)(x - x_0)$}$ die Linearisierung der Funktion $ \mbox{$f$}$ an der Stelle $ \mbox{$x_0$}$. Insbesondere entnehmen wir dieser Formulierung, daß
$ \mbox{$\displaystyle {\mbox{{$\mbox{$f$}$} differenzierbar in {$\mbox{$x_0$}$... ...htarrow \hspace*{1cm} {\mbox{{$\mbox{$f$}$} stetig in {$\mbox{$x_0$}$}}}\; . $}$
Die Umkehrung gilt nicht, wie etwa $ \mbox{$f(x) = \vert x\vert$}$ in $ \mbox{$x_0 = 0$}$ zeigt.

Die Funktion $ \mbox{$f$}$ heißt differenzierbar auf einer Teilmenge $ \mbox{$D'\subseteq D$}$, falls $ \mbox{$f$}$ in jedem $ \mbox{$x_0\in D'$}$ differenzierbar ist. Dies definiert eine Funktion $ \mbox{$f'=\frac{{\mbox{\scriptsize d}}f}{{\mbox{\scriptsize d}}x}:D'\longrightarrow \mathbb{C}$}$.

Manchmal schreibt man auch $ \mbox{$(f(x))'$}$ anstelle von $ \mbox{$f'(x)$}$.

Sind $ \mbox{$f,g:(a,b)\longrightarrow \mathbb{C}$}$ differenzierbare Funktionen mit $ \mbox{$f'=g'$}$ auf $ \mbox{$(a,b)$}$, so unterscheiden sie sich um eine Konstante. Stimmen sie darüberhinaus an einer Stelle überein, so ist $ \mbox{$f=g$}$.

Die Funktion $ \mbox{$f$}$ heißt links- bzw. rechtsseitig differenzierbar in $ \mbox{$x_0$}$, falls der Grenzwert

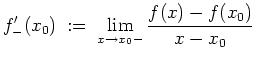
$ \mbox{$\displaystyle f'_-(x_0) \; :=\; \lim_{x\to x_0-} \frac{f(x) - f(x_0)}{x - x_0} $}$
bzw.
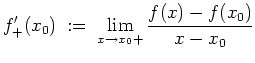
$ \mbox{$\displaystyle f'_+(x_0) \; :=\; \lim_{x\to x_0+} \frac{f(x) - f(x_0)}{x - x_0} $}$
existiert. Den Grenzwert $ \mbox{$f'_-(x_0)$}$ bzw. $ \mbox{$f'_+(x_0)$}$ nennt man diesenfalls die links- bzw. rechtsseitige Ableitung von $ \mbox{$f$}$ in $ \mbox{$x_0$}$.

Wir schreiben für die $ \mbox{$n$}$-fache Ableitung von $ \mbox{$f$}$ in einem Punkt $ \mbox{$x_0$}$

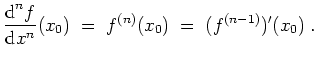
$ \mbox{$\displaystyle \frac{{\mbox{d}}^n f}{{\mbox{d}}x^n}(x_0) \;=\; f^{(n)}(x_0) \;=\; (f^{(n-1)})'(x_0) \;. $}$

Die Funktion $ \mbox{$f$}$ heißt $ \mbox{$n$}$-fach differenzierbar auf $ \mbox{$D$}$, falls $ \mbox{$f^{(n)}$}$ dort existiert.

Die Funktion $ \mbox{$f$}$ heißt $ \mbox{$n$}$-fach stetig differenzierbar auf $ \mbox{$D$}$, falls $ \mbox{$f^{(n)}$}$ dort existiert und stetig ist.

Zum Beispiel ist $ \mbox{$f(x) := x^2 \sin(1/x)$}$, stetig fortgesetzt mit $ \mbox{$f(0) := 0$}$, differenzierbar auf $ \mbox{$\mathbb{R}$}$, stetig differenzierbar aber nur auf $ \mbox{$\mathbb{R}\backslash \{ 0\}$}$.

Anschaulich gesprochen ist $ \mbox{$f'(x)$}$ die Steigung des Graphen der Funktion $ \mbox{$f$}$ an der Stelle $ \mbox{$x$}$, und $ \mbox{$f''(x)$}$ beziffert die Änderung dieser Steigung.

Monotoniekriterium.

Sei $ \mbox{$f:[a,b]\to\mathbb{R}$}$ eine stetige Funktion, die auf $ \mbox{$(a,b)$}$ differenzierbar ist, wobei $ \mbox{$a,b\in\mathbb{R}$}$ und $ \mbox{$a<b$}$.

Vorsicht, die Funktion $ \mbox{$f(x)=x^3$}$ ist auf $ \mbox{$[-1,1]$}$ streng monoton wachsend, jedoch ist $ \mbox{$f'(0)=0$}$.

Das Monotoniekriterium gilt wörtlich genauso auch für differenzierbare Funktionen auf $ \mbox{$(a,b)$}$, die in den Randpunkten nicht definiert sind.

Regeln.

Seien $ \mbox{$f,g:D\longrightarrow \mathbb{C}$}$ differenzierbar auf $ \mbox{$D'\subseteq D$}$. Dann existieren auch die folgenden Ableitungen auf $ \mbox{$D'$}$ und lassen sich wie folgt berechnen.

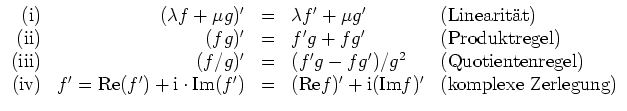
$ \mbox{$\displaystyle \begin{array}{rrcll} {\mbox{(i)}} & (\lambda f+\mu g)' &... ...rm{i}({\operatorname{Im}}f)' & {\mbox{(komplexe Zerlegung)}} \\ \end{array}$}$
Für die Quotientenregel sei dabei zusätzlich $ \mbox{$g(x)\neq 0$}$ für alle $ \mbox{$x\in D'$}$ vorausgesetzt.

Seien $ \mbox{$g:D\longrightarrow \mathbb{R}$}$ und $ \mbox{$f:E\longrightarrow \mathbb{C}$}$ differenzierbar mit $ \mbox{$g(D)\subseteq E$}$. Dann gilt die Kettenregel für $ \mbox{$f\circ g$}$ auf $ \mbox{$D$}$.

$ \mbox{$\displaystyle (f\circ g)' \;=\; (f'\circ g)\cdot g'\; , $}$
d.h. $ \mbox{$(f(g(x))'=f'(g(x))\cdot g'(x)$}$ für alle $ \mbox{$x\in D$}$.

Seien $ \mbox{$D,E\subseteq \mathbb{R}$}$ offene Mengen, und sei $ \mbox{$f:D\longrightarrow E$}$ bijektiv und differenzierbar auf $ \mbox{$D$}$ mit $ \mbox{$f'(x)\neq 0$}$ stets. Dann ist auch die Umkehrfunktion $ \mbox{$f^{-1}:E\longrightarrow D$}$ differenzierbar, und es gilt an der Stelle $ \mbox{$y_0=f(x_0)$}$

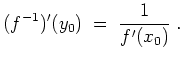
$ \mbox{$\displaystyle (f^{-1})'(y_0) \;=\; \frac{1}{f'(x_0)}\;. $}$

Standardableitungen.

Sei $ \mbox{$f(x):=\sum_{n=0}^\infty a_n (x-x_0)^n$}$ eine Potenzreihe mit $ \mbox{$a_n\in\mathbb{C}$}$, $ \mbox{$x_0\in\mathbb{R}$}$ und $ \mbox{$x\in (x_0-R,x_0+R)$}$, wobei $ \mbox{$R>0$}$ der Konvergenzradius sei. Dann dürfen wir summandenweise ableiten,

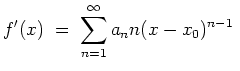
$ \mbox{$\displaystyle f'(x) \;=\; \sum_{n=1}^\infty a_n n(x-x_0)^{n-1}\; $}$
für $ \mbox{$x\in (x_0-R,x_0+R)$}$. Die Potenzreihe $ \mbox{$f'(x)$}$ hat ebenfalls den Konvergenzradius $ \mbox{$R$}$.

Insbesondere ergeben sich folgende Ableitungen.

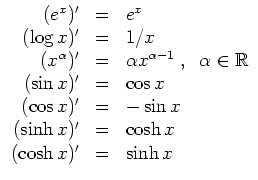
$ \mbox{$\displaystyle \begin{array}{rcl} (e^x)' &=& e^x\\ (\log x)' &=& 1/x\... ...-\sin x\\ (\sinh x)' &=& \cosh x\\ (\cosh x)' &=& \sinh x\\ \end{array}$}$
(Autoren: Künzer/Martin/Nebe)
[Beispiele] [Verweise]
  automatisch erstellt am 25.  1. 2006