
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Grenzwertregel von de l'Hospital |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Die Regel von de l'Hôpital dient der Berechnung von Grenzwerten der Form
![]() und
und
![]() .
.
Regel.
Sei
![]() eine offene Teilmenge, und seien
eine offene Teilmenge, und seien
![]() differenzierbare Funktionen, sei entsprechend
differenzierbare Funktionen, sei entsprechend
![]() im Abschluß von
im Abschluß von
![]() , aber nicht in
, aber nicht in
![]() , oder
, oder
![]() falls
falls
![]() für ein
für ein
![]() , oder
, oder
![]() falls
falls
![]() für ein
für ein
![]() . Seien
. Seien
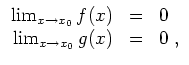
Dann gilt
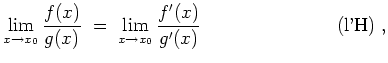
Vorsicht.
Es kann sein, daß
![]() existiert, nicht aber
existiert, nicht aber
![]() .
.
Sei z.B.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Es ist
.
Es ist
![]() . Dagegen existiert wegen
. Dagegen existiert wegen
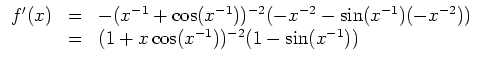
Skizze von
![]() .
.
![\includegraphics[width=10cm]{r_1.eps}](/inhalt/aussage/aussage1163/img25.png)
Skizze von
![]() .
.
![\includegraphics[width=10cm]{r_2.eps}](/inhalt/aussage/aussage1163/img27.png)
Skizze von
![]() .
.
![\includegraphics[width=10cm]{r_3.eps}](/inhalt/aussage/aussage1163/img29.png)
| automatisch erstellt am 25. 1. 2006 |