
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Partialbruchzerlegung |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Es stellt sich das Problem nach der Berechnung von Integralen des Typs
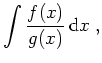
Zunächst führen wir eine Polynomdivision durch und integrieren separat zum einen das daraus hervorgehende Polynom, zum anderen
das Restpolynom, geteilt durch
![]() . Wir können in unserer Problemstellung also annehmen, daß
. Wir können in unserer Problemstellung also annehmen, daß
![]() echt kleineren Grad als
echt kleineren Grad als
![]() hat, und daß
hat, und daß
![]() normiert ist, also Leitkoeffizient
normiert ist, also Leitkoeffizient
![]() hat.
hat.
Wir bezeichnen in diesem Kapitel mit
![]() für
für
![]() das ganzzahlige Intervall.
das ganzzahlige Intervall.
Man möchte den Integranden in der Form
![$ \mbox{$\displaystyle
(\ast) \rule{3cm}{0cm} \frac{f(x)}{g(x)} \; = \; \sum_{l\in [1,k]}\;\sum_{j\in [1,m_l]} \frac{w_{l,j}}{(x - z_l)^j}
\rule{3cm}{0cm}
$}$](/inhalt/aussage/aussage1166/img8.png)
Unsere Aufgabe ist es, die Koeffizienten
![]() zu bestimmen.
zu bestimmen.
Für
![]() sei
sei
![]() .
.
Multiplizieren wir unseren Ansatz
![]() mit
mit
![]() und setzen dann
und setzen dann
![]() ein, so erhalten wir
ein, so erhalten wir
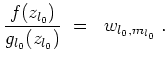
Spaltet
![]() in verschiedene Linearfaktoren auf, d.h. ist
in verschiedene Linearfaktoren auf, d.h. ist
![]() stets, dann ist man an dieser Stelle fertig.
stets, dann ist man an dieser Stelle fertig.
Ansonsten ziehe man die erhaltenen Terme auf der linken Seite ab und wende auf den Restterm
![$ \mbox{$\displaystyle
\frac{f(x)}{g(x)} - \sum_{l\in [1,k]} \frac{w_{l,m_l}}{(...
...
\; =\; \sum_{l\in [1,k]}\;\sum_{j\in [1,m_l-1]} \frac{w_{l,j}}{(x - z_l)^j}
$}$](/inhalt/aussage/aussage1166/img23.png)
Zurück zum ursprünglichen Problem. Man kann nun das Integral berechnen zu
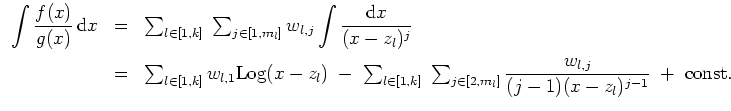
Oft können im Resultat auftretende Terme noch zusammengefaßt werden mittels
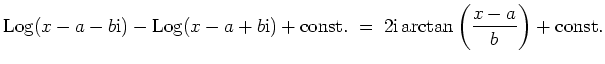
| automatisch erstellt am 25. 1. 2006 |