
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Uneigentliche Integrale |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Begriff.
Sei
![]() . Sei
. Sei
![]() stetig. Dann heißt
stetig. Dann heißt
![]() uneigentlich integrierbar, falls
das uneigentliche Integral
uneigentlich integrierbar, falls
das uneigentliche Integral
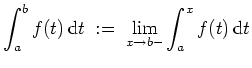
Analog ist für
![]() die stetige Funktion
die stetige Funktion
![]() uneigentlich integrierbar, falls
das uneigentliche Integral
uneigentlich integrierbar, falls
das uneigentliche Integral
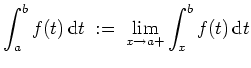
Ferner ist für
![]() die stetige Funktion
die stetige Funktion
![]() uneigentlich integrierbar, falls
das uneigentliche Integral
uneigentlich integrierbar, falls
das uneigentliche Integral
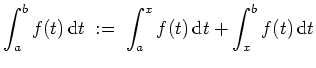
In allen Fällen heißt
![]() absolut konvergent, falls
absolut konvergent, falls
![]() konvergiert.
Konvergiert ein uneigentliches Integral absolut, so konvergiert es schlechthin.
konvergiert.
Konvergiert ein uneigentliches Integral absolut, so konvergiert es schlechthin.
Es gibt somit zwei Fälle von uneigentlichen Integralen. Zum einen können Integralgrenzen gegen
![]() oder gegen
oder gegen
![]() laufen. Zum anderen kann die Funktion an einer endlichen Stelle nicht definiert sein. (Ist an der endlichen Stelle diese Lücke stetig hebbar, so stimmt die uneigentliche Definition des Integrals mit der bisherigen überein.)
laufen. Zum anderen kann die Funktion an einer endlichen Stelle nicht definiert sein. (Ist an der endlichen Stelle diese Lücke stetig hebbar, so stimmt die uneigentliche Definition des Integrals mit der bisherigen überein.)
Intuitiv gesprochen rechnet man mit uneigentlichen Integralen Flächen aus, die endlich bleiben, obwohl der zu berechnende
Bereich ins Unendliche ragt - sei es, entlang der
![]() -Achse, sei es entlang einer vertikalen Asymptote.
-Achse, sei es entlang einer vertikalen Asymptote.
Majorantenkriterium.
Sei
![]() , sei
, sei
![]() die zu untersuchende stetige Funktion, und sei
die zu untersuchende stetige Funktion, und sei
![]() eine Majorante von
eine Majorante von
![]() , d.h. sei
, d.h. sei
![]() für alle
für alle
![]() . Falls
. Falls
![]() konvergiert,
so konvergiert
konvergiert,
so konvergiert
![]() absolut, und es ist
absolut, und es ist
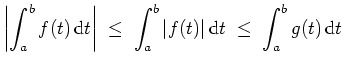
Integralkriterium für Reihen.
Sei
![]() stetig und monoton fallend. Genau dann konvergiert die Reihe
stetig und monoton fallend. Genau dann konvergiert die Reihe
![]() , wenn
, wenn
![]() konvergiert. Diesenfalls ist
konvergiert. Diesenfalls ist
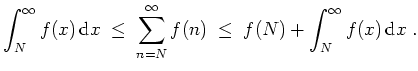
| automatisch erstellt am 25. 1. 2006 |