Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Trennbare Differentialgleichungen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Unter einer Differentialgleichung versteht man eine Gleichung, in welcher unabhängige Variablen, Funktionen in diesen unabhängigen Variablen und deren Ableitungen auftreten. Gefragt ist dabei nach diesen Funktionen.

In einer gewöhnlichen Differentialgleichung tritt nur eine unabhängige Variable, meist mit $ \mbox{$x$}$ bezeichnet, und eine Funktion, meist mit $ \mbox{$y=y(x)$}$ bezeichnet, auf.

Unter einer Lösung einer gewöhnlichen Differentialgleichung versteht man eine genügend oft differenzierbare Funktion $ \mbox{$y=y(x)$}$, welche auf einem gewissen Intervall der Differentialgleichung genügt.

Allgemeine trennbare Differentialgleichungen.

Eine trennbare Differentialgleichung ist eine Gleichung der Form

$ \mbox{$\displaystyle y' \;=\; f(x)g(y) \;. $}$
Dabei seien $ \mbox{$f$}$ und $ \mbox{$g$}$ (und alle weiteren Funktionen) stetig.

Die Lösung ergibt sich durch Integration

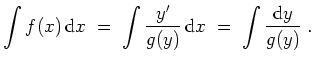
$ \mbox{$\displaystyle \displaystyle\int f(x)\,{\mbox{d}}x \;=\; \displaystyle\... ...{y'}{g(y)}\,{\mbox{d}}x \;=\; \displaystyle\int \frac{{\mbox{d}}y}{g(y)} \;. $}$
Nach Ermittlung der unbestimmten Integrale ist nach $ \mbox{$y$}$ aufzulösen, sofern möglich. Die darin auftretende Integrationskonstante liefert uns eine Lösungsschar, d.h. eine Familie von Lösungen.

Besitzt die Funktion $ \mbox{$g$}$ eine Nullstelle $ \mbox{$\eta$}$, so ist dazuhin auch die konstante Funktion $ \mbox{$y(x)=\eta$}$ eine Lösung.

Homogene lineare Differentialgleichung.

Ist speziell $ \mbox{$g(y)=y$}$, so erhält man die homogene lineare Differentialgleichung

$ \mbox{$\displaystyle y'  \;=\; f(x)y \;. $}$

Durch Integration ergibt sich nun

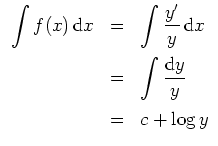
$ \mbox{$\displaystyle \begin{array}{rcl} \displaystyle\int f(x)\,{\mbox{d}}x &... ...playstyle\int \frac{{\mbox{d}}y}{y}\vspace*{2mm}\\ &=& c+\log y \end{array}$}$
mit einer Konstanten $ \mbox{$c\in\mathbb{R}$}$. Auflösen nach $ \mbox{$y$}$ ergibt
$ \mbox{$\displaystyle y \;=\;  C e^{F(x)} $}$
mit einer Stammfunktion $ \mbox{$F(x)=\int f(x)\,{\mbox{d}}x$}$ und einer Konstanten $ \mbox{$C\in\mathbb{R}$}$.

Inhomogene lineare Differentialgleichung.

Wir betrachten eine Gleichung der Form

$ \mbox{$\displaystyle y'  \;=\; f(x)y + h(x)\;. $}$

Die allgemeine Lösung dieser inhomogenen linearen Differentialgleichung ergibt sich als Summe einer partikulären Lösung dieser inhomogenen Gleichung und der allgemeinen Lösung der zugehörigen homogenen Gleichung $ \mbox{$y'=f(x)y$}$.

Die Lösung der zugehörigen homogenen Gleichung ergibt sich wie oben zu $ \mbox{$y= Ce^{F(x)}$}$.

Die partikuläre der inhomogenen Gleichung Lösung ergibt sich durch Variation der Konstanten. Wir betrachten $ \mbox{$C=C(x)$}$ als Funktion von $ \mbox{$x$}$, setzen $ \mbox{$y=C(x)e^{F(x)}$}$ in die inhomogene Gleichung ein und erhalten

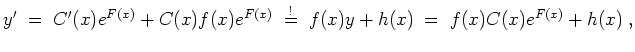
$ \mbox{$\displaystyle y' \;=\; C'(x)e^{F(x)} + C(x)f(x)e^{F(x)} \;\stackrel{!}=\; f(x)y+h(x) \;=\; f(x)C(x)e^{F(x)}+h(x) \;, $}$
und somit
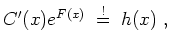
$ \mbox{$\displaystyle C'(x)e^{F(x)} \;\stackrel{!}=\; h(x) \;, $}$
d.h.
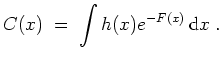
$ \mbox{$\displaystyle C(x) \;=\; \displaystyle\int h(x)e^{-F(x)}\,{\mbox{d}}x \;. $}$
Die allgemeine Lösung der inhomogenen Gleichung ist also
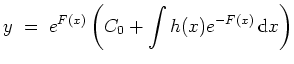
$ \mbox{$\displaystyle y \;=\; e^{F(x)}\left(C_0 +\displaystyle\int h(x)e^{-F(x)}\,{\mbox{d}}x \right) $}$
mit einer Konstanten $ \mbox{$C_0\in\mathbb{R}$}$.
(Autoren: Künzer/Martin/Nebe)
[Beispiele] [Verweise]
  automatisch erstellt am 25.  1. 2006