Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Leonhard Euler

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Leonhard Euler wurde am 15. April 1707 in Basel geboren. Auf Wunsch seines Vaters begann er 1723, an der Universität Basel Theologie zu studieren. Mit Hilfe von Johann Bernoulli konnte er seinem Vater aber die Erlaubnis abringen, zur Mathematik wechseln zu dürfen. 1726 beendete er sein Studium und war von 1727 bis 1741 Mitglied der St. Petersburger Akademie der Wissenschaften. Von 1741 bis 1766 war er an der Preußischen Akademie in Berlin tätig, kehrte dann wieder nach St. Petersburg zurück, wo er am 18. September 1783 verstarb.

Euler hat im Laufe seines Lebens über 800 Veröffentlichungen zu vielen unterschiedlichen Bereichen der Mathematik verfasst.

Die Schreibweisen $ f(x)$ für eine Funktion, $ e$ für die Basis des natürlichen Logarithmus, $ \mathrm{i}$ für die imaginäre Einheit und $ \sum$ für Summen gehen auf Euler zurück.

Auf dem Gebiet der Zahlentheorie hat Euler gezeigt, dass die fünfte Fermatsche Zahl ( $ 2^{2^5}+1 =4294967297$) durch $ 641$ teilbar ist. Er widerlegte damit die Vermutung, dass alle Zahlen der Bauart $ 2^{2^n}+1$ prim sind. Außerdem führte er die $ \phi$-Funktion ein ($ \phi(n)$ ist die Zahl der zu $ n$ teilerfremden Zahlen $ <n$) und erweiterte den kleinen Fermatschen Satz ( $ a^p=a \operatorname{mod} p$) auf $ a^{\phi(n)} = 1 \operatorname{mod} n$, worauf der RSA-Verschlüsselungsalgorithmus beruht.

Für die Riemannsche Zeta-Funktion fand er die Darstellung

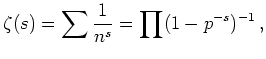
$\displaystyle \zeta(s) =\sum \frac{1}{n^s} = \prod (1-p^{-s})^{-1}\,, $

wobei die Summe über alle natürlichen Zahlen $ n$ und das Produkt über alle Primzahlen $ p$ gebildet wird. Er berechnete $ \zeta(2n)$ für $ n=1$ bis $ 13$ und fand eine allgemeine Darstellung für $ \zeta(2n) = c\pi^{2n}$, wobei $ c$ mit Hilfe von Bernoulli-Zahlen ausgedrückt wird.

1735 führte er die nach ihm benannte Konstante

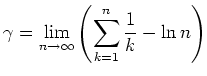
$\displaystyle \gamma = \lim\limits_{n\to \infty} \left(\sum\limits_{k=1}^n \frac{1}{k} - \ln n \right) $

ein und berechnete sie auf 16 Dezimalstellen.

Er war 1744 auch der erste, der eine Fourier-Reihe für eine Funktion angab:

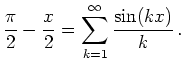
$\displaystyle \frac{\pi}{2}-\frac{x}{2} = \sum\limits_{k=1}^\infty \frac{\sin(kx)}{k}\,. $

Er hat noch viele weitere Beiträge zur Mathematik geleistet, beispielsweise

(Autor: Hörner)
[Verweise]
  automatisch erstellt am 25.  1. 2006