Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Rotation von Kegelschnitten

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Transformiert man den Kegelschnitt mit der Gleichung

$\displaystyle ax^2 + bxy + cy^2 + dx + ey +f = 0 $

mittels einer Rotation um den Ursprung mit positvem Winkel $ \alpha $ dann erhält man für

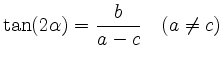
$\displaystyle \tan (2\alpha) = \frac{b}{a-c} \quad (a \neq c)$

bzw. für

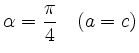
$\displaystyle \alpha = \frac{\pi}{4} \quad (a = c)$

eine Gleichung, in der der gemischte quadratische Term den Koeffizienten 0 besitzt, also in neuen Koordinaten $ \tilde{x}, \tilde{y}$ eine Gleichung der Form

$\displaystyle \tilde{a}\tilde{x}^2 + \tilde{c}\tilde{y}^2 + \tilde{d}\tilde{x} + \tilde{e}\tilde{y} + \tilde{f} = 0 .$

Die durch die Rotation bestimmte Koordinatentransformation, die die alten Kooordinaten in den neuen ausdrückt, hat die Gestalt

$\displaystyle x= \tilde{x}\cos \alpha - \tilde{y}\sin \alpha \,,\quad y= \tilde{x}\sin \alpha + \tilde{y}\cos \alpha \,. $

Die Parameter der neuen Gleichung berechnen sich zu

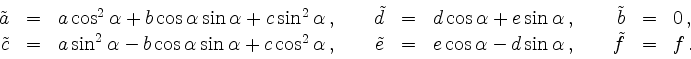
\begin{displaymath} \begin{array}{rclcrclcrcl} \tilde{a} &=& a \cos^2 \alpha +... ...ha - d \sin \alpha \,,&\ & \tilde{f} &=& f\,.\\ \end{array} \end{displaymath}

Man beachte, dass die neue Gleichung durch quadratische Ergänzung leicht in eine Normalform des Kegelschnitts übergeführt werden kann.

siehe auch:

  automatisch erstellt am 28.  3. 2008