Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Gauß-Jordan-Algorithmus

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Mit dem Gauß-Jordan-Algorithmus kann ein lineares Gleichungssystem

$\displaystyle Ax = b $

mit einer nicht singulären $ n\times n$ Koeffizientenmatrix $ A$ gelöst werden. Dazu eliminiert man durch Äquivalenzumformungen sukzessive die Unbekannten

$\displaystyle x_\ell \,, \quad \ell=1, \ldots ,n\,, $

so dass die Koeffizientenmatrix zur Einheitsmatrix wird und die rechte Seite die Lösung $ x$ enthält.

Zur Durchführung des Algorithmus fasst man die Koeffizientenmatrix und die rechte Seite zu einer $ n \times (n+1)$ Matrix $ W=(A,b)$ zusammen. Vor dem $ \ell$-ten Eliminationsschritt hat diese erweiterte Matrix dann die Form

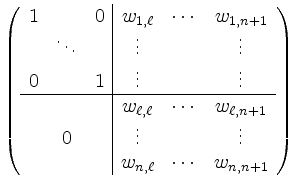
$\displaystyle \left( \begin{array}{ccc\vert ccc} 1 & & 0 & w_{1,\ell} & \cdots&... ...vdots & & \vdots \\ & & & w_{n,\ell} & \cdots& w_{n,n+1} \end{array} \right) $

mit modifizierten Elementen $ w_{i,j}$.

Die Elimination von $ x_\ell$ verläuft in drei Schritten:

  1. Bestimmung eines Maximums $ \vert w_{i,\ell}\vert$ der Beträge von $ w_{\ell,\ell} , \ldots , w_{n,\ell}$ und Vertauschung der Zeilen $ \ell$ und $ i$,
  2. Division der Zeile $ \ell$ durch $ w_{\ell,\ell}$,
  3. Subtraktion des $ w_{j,\ell}$-fachen der Zeile $ \ell$ von den Zeilen $ j$ für $ j \neq \ell$:

    $\displaystyle w_{j,k} \longleftarrow w_{j,k} -w_{j,\ell} \; w_{\ell,k}\,, \quad k=\ell,\ldots,n+1 \,. $

Durch den dritten Schritt werden Nullen in den Positionen $ (j,\ell)\,,\; j\neq \ell$, erzeugt, d.h. die Dimension der Einheitsmatrix im linken oberen Block wird um eins vergrößert. Folglich enthält die Spalte $ n+1$ von $ W$ nach $ n$ Eliminationsschritten die Lösung $ x$.

[Downloads] [Beispiele] [Verweise]
  automatisch erstellt am 19.  8. 2013