Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Lösen eines linearen Gleichungssystems in Dreiecksform

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Ein lineares Gleichungsssystem in der Dreiecksform

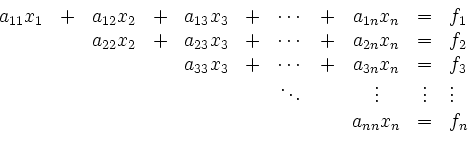
\begin{displaymath} \begin{array}{rcrcrcccccl} a_{11}x_1 &+& a_{12}x_2 &+& a_{13... ...ots \\ & & & & & & & & a_{nn}x_n &=& f_n \\ \par \end{array}\end{displaymath}

lässt sich eindeutig lösen, wenn $ a_{ii}\neq 0$ für $ i=1,2,3,\dots,n$.

Die Lösung lässt sich durch Rückwärtseinsetzen bestimmen. So folgt aus der letzten Gleichung $ x_n=f_n/a_{nn}$. Durch Einsetzen dieser Darstellung in die vorletzte Gleichung kann $ x_{n-1}$ berechnet werden. Dies kann nun sukzessive weitergeführt werden, bis man abschließend mit Hilfe der ersten Gleichung $ x_1$ erhält.

(Autor: J. Wipper)

siehe auch:

  automatisch erstellt am 12.  5. 2006