Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Klammerung und Gruppierung von mathematischen Ausdrücken in LaTeX

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Zur Klammerung bzw. Gruppierung stellt LATEX die folgenden skalierbaren Symbole zur Verfügung
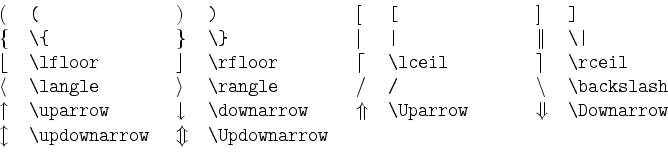
\begin{tabular}{lp{2.7cm}lp{2.7cm}lp{2.7cm}lp{2.7cm}} $($\ & \verb\vert(\vert &... ...pdownarrow\vert & $\Updownarrow$\ & \verb\vert\Updownarrow\vert \end{tabular}
Eine automatische Skalierung erfolgt mit Hilfe der Befehle
\leftSymbol    Ausdruck     \rightSymbol.
Die beiden Befehle \left und \right müssen immer paarweise verwendet werden. Die angegebenen Symbole werden dabei automatisch auf die Größe des eingeschlossenen mathematischen Ausdrucks skaliert. Die beiden bei \left und \right angegebenen Symbole müssen nicht übereinstimmen. Insbesondere kann durch Angabe eines Punktes an Stelle des anderen Symbols eine einseitige Klammer erzeugt werden. Die Schachtelung von Klammerungen ist erlaubt. So erzeugt beispielsweise der Quelltext 
  \[ 
    \int_0^1 \left(\frac{x^2}{2}-x\right)e^x\,dx
    =\left[\left(\frac{x^2}{2}-x\right)e^x\right]_0^1
    -\int_0^1\left(x-1\right)e^x\,dx
  \]
die Ausgabe

$\displaystyle \int_0^1 \left(\frac{x^2}{2}-x\right)e^x\,dx =\left[\left(\frac{x^2}{2}-x\right)e^x\right]_0^1 -\int_0^1\left(x-1\right)e^x\,dx\,. $

Für die manuelle Skalierung stehen die Befehle

\bigSymbol      \BigSymbol      \biggSymbol      \BiggSymbol
zur Verfügung, die auch einzeln (also nicht nur paarweise) verwendet werden dürfen. So ergibt zum Beispiel 
  \[
    \Bigg(\,\bigg(\,\Big(\,\big(\,(\,)\,\big)\,\Big)\,\bigg)\,\Bigg) \qquad
    \Bigg[\,\bigg[\,\Big[\,\big[\,[\,]\,\big]\,\Big]\,\bigg]\,\Bigg] \qquad
    \Bigg\{\,\bigg\{\,\Big\{\,\big\{\,\{\,\}\,\big\}\,\Big\}\,\bigg\}\,\Bigg\} 
  \]
die Ausgabe

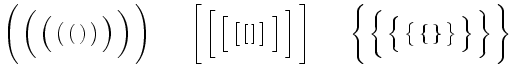
$\displaystyle \Bigg(\,\bigg(\,\Big(\,\big(\,(\,)\,\big)\,\Big)\,\bigg)\,\Bigg) ... ...ad \Bigg\{\,\bigg\{\,\Big\{\,\big\{\,\{\,\}\,\big\}\,\Big\}\,\bigg\}\,\Bigg\} $

Die manuelle Größenanpassung ist insbesondere zur besseren Gruppierung gleichgroßer Objekte, wie etwa bei

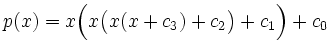
$\displaystyle p(x)=x\Big(x\big( x(x+c_3)+c_2\big)+c_1\Big)+c_0 $

geeignet, bei denen die Verwendung von \left( und \right) bzw. normaler Klammern das weniger übersichtliche Ergebnis

$\displaystyle p(x)=x\left(x\left(x\left(x+c_3\right)+c_2\right)+c_1\right)+c_0 $

liefert.

Mit Hilfe der Befehle

\underbrace{Ausdruck}     bzw.      \overbrace{Ausdruck}
können horizontale geschweifte Klammern unter bzw. über einen Ausdruck gesetzt werden. Ein anschließend tief- bzw. hochgestellter Ausdruck erscheint unter bzw. über der Klammer.

So erzeugt beispielsweise der Quelltext 

  \[
    \sum_{k=1}^n \overbrace{\cos (\pi k)}^{=(-1)^k} k^2 
    =\underbrace{-1+4-9+\dots +(-1)^n n^2}_{n\text{\ Summanden}}
  \]
die Ausgabe

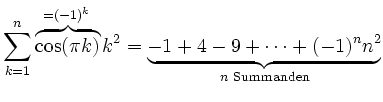
$\displaystyle \sum_{k=1}^n \overbrace{\cos (\pi k)}^{=(-1)^k} k^2 =\underbrace{-1+4-9+\dots +(-1)^n n^2}_{n\text{ Summanden}} $

Die Schachtelung von \underbrace und \overbrace ist erlaubt.

(Autor: Joachim Wipper)
[Beispiele] [Verweise]
  automatisch erstellt am 22.  6. 2006