Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Elementarmatrix

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Sei $ E_{ij}$ die n$ \times$n-Matrix, die im Schnittpunkt der i-ten Zeile und der j-ten Spalte eine 1, sonst überall 0 hat. Als Elementarmatrizen werden bezeichnet:
  1. $ F_{ij}(\alpha) := E_{n} + \alpha E_{ij}$ für $ \alpha \in K$ und $ 1\leq i \not= j \leq n$
  2. $ F_{i}(\alpha) := E_{n} + (\alpha-1)E_{ii}$ für $ \alpha \in K^{\times}$ und $ 1 \leq i \leq n.$

Es gilt also
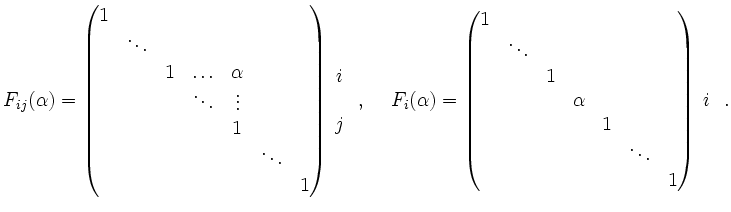
$ F_{ij}(\alpha) = \begin{pmatrix}1 & & & & & & \\ & \ddots & & & & & \\ & & 1 ... ...0.1cm} \begin{matrix}\\ \\ i \\ \\ \\ \end{matrix}\hspace{0.3cm}.\vspace{1.5cm}$

Durch leichtes Nachrechnen sieht man, dass $ \hspace{0.3cm}F_{ij}(\alpha), \hspace{0.1cm} F_{i}(\alpha) \in$ GL(n,K) und

$\displaystyle F_{ij}(\alpha)^{-1} = F_{ij}(- \alpha) \hspace{0.3cm}(\alpha \in K),$

$\displaystyle F_{i}(\alpha)^{-1} = F_{i}(\alpha ^{-1}) \hspace{0.3cm}(\alpha \in K^{\times}).$


Multiplikation einer Matrix $ A$ von links (rechts) mit $ F_{i}(\alpha)$ bedeutet Multiplikation der i-ten Zeile (Spalte) mit $ \alpha$,
Multiplikation der Matrix $ A$ von links (rechts) mit $ F_{ij}(\alpha)$ bedeutet Addition des $ \alpha$-fachen der j-ten Zeile (i-ten Spalte)
zur i-ten Zeile (j-ten Spalte). Man spricht von ´´elementaren Zeilen- bzw. Spaltenumformungen``.

(Autor: Borgart)

siehe auch:

  automatisch erstellt am 6. 10. 2006