Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

QR-Faktorisierung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Eine beliebige ALT=-Matrix ALT= kann, gegebenenfalls nach einer Permutation der Spalten, als Produkt einer orthogonalen Matrix ALT= und einer oberen Dreiecksmatrix ALT= faktorisiert werden:

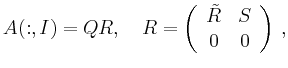
$\displaystyle A(:,I)=QR,\quad R = \left(\begin{array}{cc} \tilde R & S \\ 0 & 0 \end{array}\right) \,, $

mit einem Indexvektor $ I$ und einer quadratischen invertierbaren oberen Dreiecksmatrix $ \tilde R$. Die Dimension von $ \tilde R$ ist der Rang von ALT=.

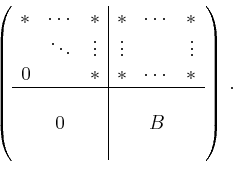
Die QR-Zerlegung lässt sich mit maximal $ \min(m,n-1)$ Householder-Transformationen konstruieren:

$\displaystyle Q=\left( \cdots Q_2 Q_1 \right)^{-1}=Q_1 Q_2 \cdots \,. $

Vor der $ \ell$-ten Transformation hat die Matrix $ Q_\ell \cdots Q_1 A(:,I)$ die Form

\begin{displaymath} \left( \begin{array}{ccc\vert ccc} * & \cdots & * & * & \... ...\ & 0 & & & B & \\ & & & & & \end{array} \right) \,. \end{displaymath}

Falls $ B$ die Nullmatrix ist, ist die obere Dreiecksform erreicht. Anderenfalls werden zwei Spalten vertauscht, so dass die $ 2$-Norm der ersten Spalte $ c$ von $ B$ maximal ist. Dann wird die durch $ c$ bestimmte Householder-Transformation auf $ B$ angewandt.

Die Permutationen werden in einem Indexvektor $ I$ abgespeichert, der mit $ (1, \ldots,m)$ initialisiert wird. Bei einer Spaltenvertauschung werden dann die entsprechneden Indizies in $ I$ vertauscht.

Download:

(Dateityp: .m, 469 ,  03.05.2010)
[Beispiele] [Verweise]
  automatisch erstellt am 19.  8. 2013