Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Integrationsformeln für Simplizes

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Für einen $ m$ -dimensionalen Simplex $ S$ mit Ecken $ v_0,\ldots,v_m$ lässt sich eine Integrationsformel durch Interpolation mit Poynomen vom totalen Grad $ \le n$ konstruieren. Das interpolierende Polynom ist eindeutig durch die Werte an den Punkten

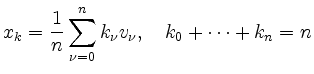
$\displaystyle x_k = \frac{1}{n}\sum_{\nu=0}^n k_\nu v_\nu,\quad k_0 + \cdots + k_n = n $

bestimmt, die ein regelmäßiges Gitter bilden. Mit $ \left(\mathrm{vol}S\,w_k \right)$ den Integralen über die Lagrange-Polynome zu $ x_k$ ist

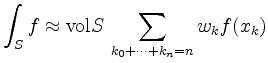
$\displaystyle \int_S f \approx \mathrm{vol}S\, \sum_{k_0+\cdots+k_n=n} w_k f(x_k) $

eine Approximation der Ordnung $ n+1$ , d.h. die Integrationsformel ist exakt für alle Polynome vom totalen Grad $ \le n$ .


\includegraphics[width=0.7\linewidth]{Bild_Integration_Simplex.eps}

\includegraphics[width=0.7\linewidth]{Bild1_Integration_Simplex.eps}

Die Abbildung zeigt die Punkte und Gewichte für die ersten Formeln in zwei und drei Dimensionen auf dem Standardsimplex ( $ \mathrm{vol} S = 1$ ).

Für allgemeine Gebiete kann die Integrationsformel auf den Simplizes einer Triangulierung angewendet werden. Der Fehler hat dann die Ordnung $ O(h^{n+1})$ , wobei $ h$ den maximalen Durchmesser der Teilsimplizes bezeichnet.

siehe auch:

[Erläuterungen]
  automatisch erstellt am 19.  8. 2013