Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Rationale Funktion

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Eine rationale Funktion $ r$ mit Zählergrad $ m$ und Nennergrad $ n$ ist der Quotient zweier Polynome:

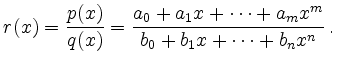
$\displaystyle r(x) = \frac{p(x)}{q(x)} = \frac{a_0+a_1x+\cdots+a_mx^m}{b_0+b_1x+\cdots+b_nx^n} \,. $

Diese Darstellung bezeichnet man als irreduzibel, wenn $ p$ und $ q$ keinen gemeinsamen Linearfaktor besitzen. Die Nullstellen des Nenners sind dann Definitionslücken der rationalen Funktion $ r$ und werden als Polstellen bezeichnet. Ihre Ordnung entspricht der Vielfachheit der Nullstelle.

Die Variable $ x$ und die Koeffizienten $ a_k$, $ b_k$ können reell oder komplex sein. Entsprechend spricht man von einer reellen oder komplexen rationalen Funktion.

Beispiele:

[Verweise]
  automatisch erstellt am 19.  8. 2013