Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Neuronales Netz

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Neuronale Netze werden dazu benutzt, um komplizierte Entscheidungsmechanismen zu simulieren. Typischerweise sollen dabei aus Eingabewerten $ (x_1,\ldots,x_m)$ optimale Ausgabewerte $ (y_1,\ldots,y_n) = f(x)$ berechnet werden. Die Funktion $ f$ ist nicht bekannt, es existiert jedoch ein Datensatz $ (x,f(x))$, $ x\in D\,,$ bekannter Werte.

Zur Approximation wird eine von Parametern $ A$ abhängige Funktion $ f_A$ gewählt und dabei versucht, die Parameter $ A$ mit Hilfe des Datensatzes zu bestimmen. Eine naheliegende Möglichkeit dazu ist die Lösung des Ausgleichsproblems

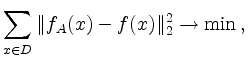
$\displaystyle \sum_{x\in D} \Vert f_A(x) - f(x)\Vert _2^2 \to \min \,, $

wobei die Menge der Test- oder Lerndaten auch sukzessive erweitert werden kann.

\includegraphics[width=0.5\linewidth]{Bild_neuronales_Netz.eps}

In dem abgebildeten Modell ist die Funktion $ f_A$ mit Hilfe von Teilabbildungen und Zellen (Neuronen) definiert:

$\displaystyle x=z^0 \mapsto z^1 \mapsto \cdots \mapsto z^\ell = y \,. $

Dabei ist, wie in der Abbildung angedeutet,

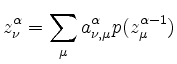
$\displaystyle z_\nu^\alpha = \sum_\mu a_{\nu,\mu}^\alpha p(z_\mu^{\alpha-1}) $

mit $ p$ einer geeignet gewählten nichtlinearen Funktion, die sich an biologischen Prozessen orientieren soll. Eine mögliche Wahl ist $ p(t) = 1/(1+\exp(-p_1 t)) + p_2$. Die Parameter $ a_{\nu,\mu}^\alpha$ sind in dem Tensor $ A$ zusammengefasst.

In dem beschriebenen Modell entspricht der Lernprozess einem nichtlinearen Ausgleichsproblem zur Bestimmung von $ A$, das mit Methoden der globalen Minimierung gelöst werden kann.

(Autoren: Höllig/Hörner/Pfeil )

siehe auch:

  automatisch erstellt am 18.  1. 2008