Mathematik-Online-Lexikon: Konjugierte Gradienten von Fletcher und Reves

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Lexikon:
	Konjugierte Gradienten von Fletcher und Reves

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Übersicht

Das Verfahren der konjugierten Gradienten bestimmt bei exakter Rechnung das Minimum einer quadratischen konvexen Funktion von Variablen in höchstens Schritten. Fletcher und Reves formulierten den Algorithmus so, dass er auf beliebige glatte Funktionen angewendet werden kann.

Ausgehend von Startwerten

$\displaystyle x_0,\quad g_0 = \operatorname{grad}f(x_0),\quad d_0 = -g_0$

generiert man eine Folge von Näherungen $x_\ell$ für eine Minimalstelle und Suchrichtungen $d_\ell$ durch folgende Rekursionen:

$x_{\ell+1} = x_{\ell} + \alpha_\ell d_\ell$ mit $\alpha_\ell>0$ bestimmt durch Minimierung von $f(x_{\ell} + \alpha d_\ell)$ für $\alpha>0$ ,
$g_{\ell+1} = \operatorname{grad}f(x_{\ell+1})$ ,
$d_{\ell+1} = -g_{\ell+1} + \beta_\ell d_\ell$ , $\beta_\ell = g_{\ell+1}^\mathrm{t} g_{\ell+1} / g_{\ell}^\mathrm{t} g_{\ell}$ .

Der einzige Unterschied zum quadratischen Fall ist, dass $\alpha_\ell$ nicht explizit bestimmt werden kann.

Ein gute Performance kann besonders dann erzielt werden, wenn gut durch eine quadratische konvexe Funktion approximiert wird. Ist dies nicht der Fall, so sollte in geeigneten Abständen ein Neustart des Verfahrens erfolgen.

Die eindimensionale Minimierung wird im allgemeinen nicht exakt durchgeführt. Dann ist jedoch darauf zu achten, dass

$\displaystyle g_{\ell+1}^\mathrm{t} d_{\ell+1} < 0 \,,$

d.h., dass die Suchrichtungen lokale Abstiegsrichtungen sind. Ist $x_{\ell+1}$ ein lokales Minimum von

in Richtung $d_\ell$ , so gilt $g_{\ell+1}^\mathrm{t}d_\ell=0$ , so dass aufgrund der Definition von $d_{\ell+1}$ diese Bedingung automatisch erfüllt ist.

Es existieren einige Varianten bei der Parameterwahl, die ebenfalls mit dem quadratischen Fall konsistent sind. Beispielsweise definieren Polak und Ribiere

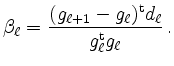
$\displaystyle \beta_\ell = \frac{(g_{\ell+1}-g_{\ell})^\mathrm{t}d_\ell}{ g_\ell^\mathrm{t} g_\ell} \,.$

Diese Wahl führt oft in der Praxis zu besseren Ergebnissen als die klassische Variante von Fletcher und Reves.

[Verweise]

automatisch erstellt am 19. 8. 2013