Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Adjunkte

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Es sei $ A\in K^{n\times n}$ eine Matrix über dem Körper $ K$. Dann bezeichnet $ \tilde{A}_{ij}$ diejenige $ ((n-1) \times (n-1))$-Untermatrix von $ A$, die aus $ A$ durch Streichen der $ i$-ten Zeile und der $ j$-ten Spalte entsteht.
Unter der Adjunkten $ \tilde{a}_{ij}$ von $ A$ versteht man die vorzeichenbehaftete Unterdeterminante bezüglich $ a_{ij}$:

$\displaystyle \tilde{a}_{ij} := (-1)^{i+j} \cdot \det \tilde{A}_{ij} $

Anstatt für jede Adjunkte das Vorzeichen nach $ (-1)^{i+j}$ zu berechnen, kann man auch ein über die Matrix verteiltes Vorzeichenmuster benutzen:

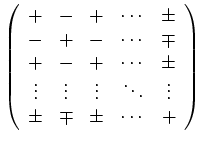
$\displaystyle \left( \begin{array}{ccccc} + & - & + & \cdots & \pm \\ - & + & ... ...& \vdots & \ddots & \vdots \\ \pm & \mp & \pm & \cdots & + \end{array}\right) $

siehe auch:

  automatisch erstellt am 25.  1. 2006